SuperZLW's Blog

我很笨，但是我不懒

0%

三维重建基础与极几何

发表于 分类于 Valine：

引入

一般做三维重建我们是采用多视图的，单视图虽然也能做，但需要有场景的先验信息，比如点的对应关系，线、面几何等，所以在条件允许的情况下，基于多视图的三维重建适用范围是要优于单视图的，这里介绍两视图的情况，包括它们包含的几何关系。

三角测量(Triangulation)

我们想要解决的问题是：

现给定一个三维点在两个或多个图像(相机矩阵已知)中的投影，希望找到该点的坐标。

以两图像投影为例，如下图：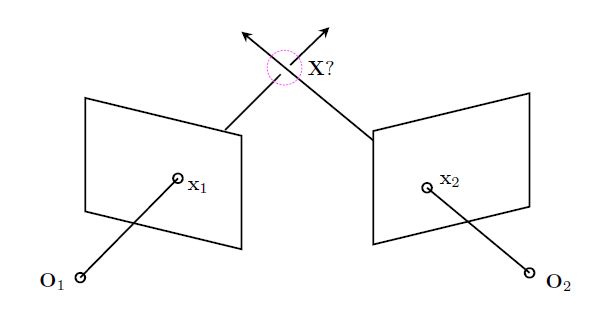
正常来说，由于相机矩阵是已知的，$O_1x_1$和$O_2x_2$我们都能表示出来，也就很容易求出这个空间三维点$X$了，然而这有个前提，就是那两条视线应该相交，但由于噪音和数值误差，这个条件一般都不能满足。\
也就是说一般情况下是这样子的：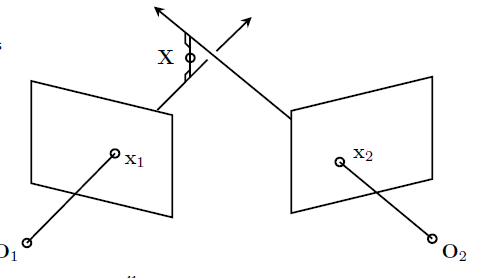
我们的想法是：找到连接两条视线的最短线段，并让 X 为该线段的中点。具体操作为：

  1. 寻找线段的方向(即垂直于两条射线);
  2. 构造两个平面，每个平面都包含该线段以及一条射线;
  3. 将该平面与其它射线相交以产生线段的端点;
  4. 找到中点。

找是找到了这个点，怎么求呢，我们现在已知的条件有：$x_1,x_2$，内参矩阵$K_1,K_2$，旋转平移$R,T$(也就是知道投影矩阵)，这里主要有两种方法，线性法和非线性法。

线性法

线性法的话，精度不高但比较容易。\
由共线可知：

这明显就是个齐次线性方程组，用SVD分解很快就做出来了，这在之前相机那篇已经介绍过，这里就不赘述了，链接在这。 \
对于多于两个视图的情况，无非就是多列几个方程。

非线性法

这种方法简单说就是希望找到个$X$，使其最小化下面这个式子：

如图：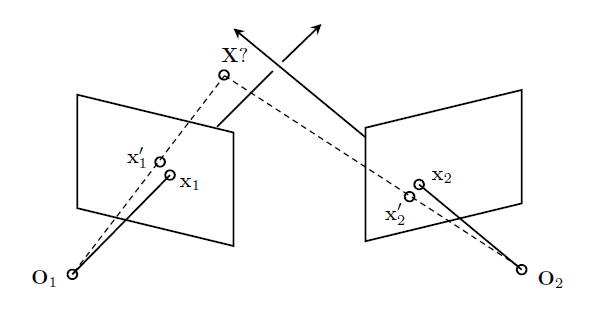
也即是说，我们要找的那个三维点，它投影到图像上的点，要跟我们观测点距离最小。也就是图中的最小。\
假设我们把世界坐标系设在$O_1$的位置，那么两个投影矩阵分别为：

至此条件都足够了，然后通过迭代求解就行，一般是用高斯牛顿法或者L-M法求解，这个在另一篇非线性优化里也已经介绍过了，链接在这。 \

极几何

接下来我们想知道的就是同一场景的两个不同视图之间的关系。\
这里先给几个后面需要用到的概念：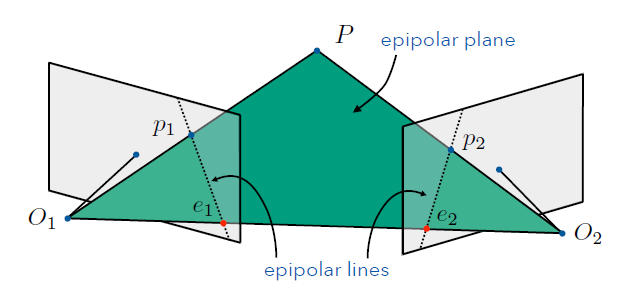

  1. 极平面(Epipolar plane): 过点$P$与两相机中心的平面;
  2. 基线(baseline): $O_1$与$O_2$的连线;
  3. 极线(epipolar lines): 极平面与成像平面的交线，也就是$p_1e_1$和$p_2e_2$;
  4. 极点(Epipole): 基线与成像平面的交点，也就是$e_1$和$e_2$。(可以在可见区域之外)

现在来看这个图：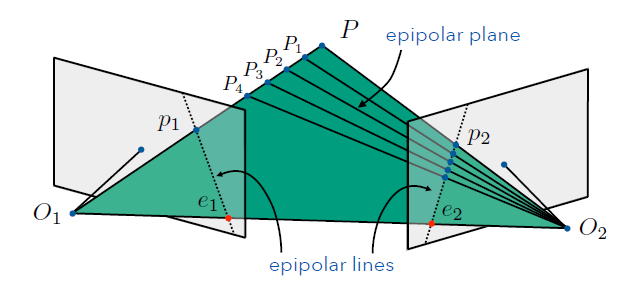
关于这个极几何有几个性质需要提一下(第3,4点比较重要):

  1. 极平面相交于基线;
  2. 极线相交于极点;
  3. $p_1$的对应点落在极线$p_2e_2$上;
  4. $p_2$的对应点落在极线$p_1e_1$上;

最后两个性质表明，我们要找一个像点在另一个平面的对应点时，不用整张图去找，只要找极线就行了。\
来看几个特例：\
(1). 平行视图：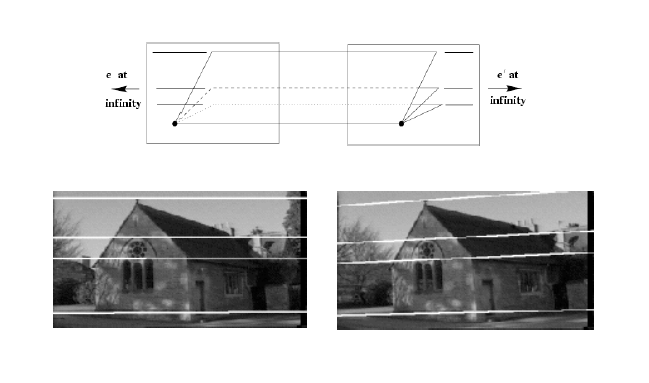

两个图像平行；\
基线平行于图像平面，两极点位于无穷远处；\
极线平行于图像坐标轴的其中一条轴。\

(2). 前后平移：

两幅图极点位置相同，极点称为展开焦点。

极几何约束

现在我们想要知道的是，一个图中的点和另一幅图中点的对应关系。\
如下图：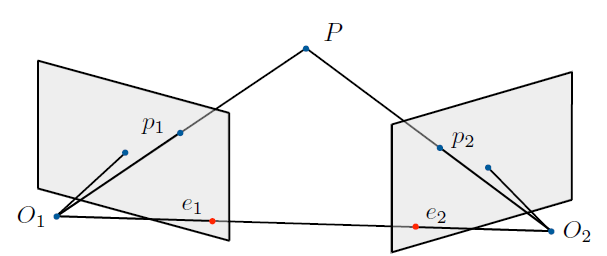
明显，我们有如下关系(这些关系都是等价的，一个意思)：

  1. $\overrightarrow{O_1P},\overrightarrow{O_2P},\overrightarrow{O_1O_2}$ 共面;\
  2. $\overrightarrow{O_1p_1},\overrightarrow{O_2p_2},\overrightarrow{O_1O_2}$ 共面;\
  3. $\overrightarrow{O_1p_1}\cdot [\overrightarrow{O_1O_2}\times \overrightarrow{O_2p_2}]=0$。

本质矩阵情况下

这种情况我们考虑的是规范化相机，规范化相机是指相机内参数矩阵为单位矩阵的相机，即是：

假设$p_1=(u_1,v_1,1)^T$，$p_2=(u_2,v_2,1)^T$，上面最后一个关系(3)就等价于：

上面这个呢就是外极性约束了。\
叉乘的话可以表示成矩阵形式，比如说

所以本质矩阵：$E=[t]_{\times}R$\
将上面那个外极性约束用本质矩阵描述的话是:

也就是说空间一个三维点在双视图中必须满足 $p_1^TEp_2=0$。\
随着这个本质矩阵带来的，还有下面一系列的重要性质：

  1. 极线用本质矩阵可表示为：$l_1=Ep_2$, $l_2=E^Tp_1$;
  2. $e_1^TE=E^Te_1=0$与$Ee_2=0$;
  3. 本质矩阵是奇异的，秩为2; 剩下的两个特征值相等;
  4. 本质矩阵有5个自由度(三个旋转+三个平移，但$det(E)=0$去掉了一个，或者说由于比例是任意的，所以去掉了一个)。

(上面4个性质都容易证明，就不写了，但有一个性质需要记住：反对称矩阵的秩是偶数的)\

举个平行相机的例子，如图：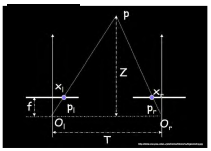
由于是平行的，$R=I$，平移量为$b$，则$t=[-b,0,0]$，所以本质矩阵为：

由约束条件 $p_{1}^TEp_2=0$ 得：

解得：$y_1=y_2$, $x_2$ 任意。

基础矩阵情况下

一般情况下我们的相机都不是规范化的相机，而是普通的一般化相机，不适用于上面的情况，这时候就引出了与本质矩阵相对的“基础矩阵”。\
依旧是这个图：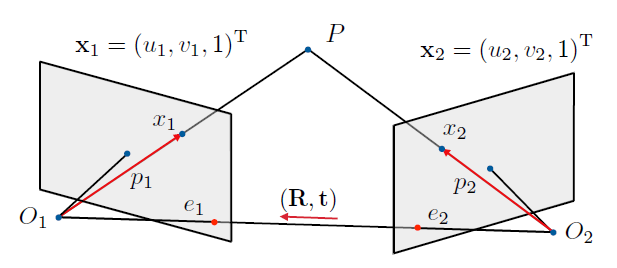
但这时候的$K$不再是单位矩阵了，怎么做？\
最直接的想法就是把它转化为规范化相机。\
我们假设两个内参矩阵分别是:$K_1,K_2$，这两个是已知的。然后有如下关系：

即是:

设：$K^{-1}x_1=x_{1c}$, 所以有：

同理，$K_2^{-1}x_2=x_{2c}$
如此得出来的$x_{1c},x_{2c}$就是规范化相机下$P$的对应点。\
文字描述的话就是：把成像平面上实际观测点乘以该相机内参数矩阵的逆矩阵，就可以得到对应的规范化相机下的点。\
由本质矩阵的性质有:

中间这串就是我们要引出的基础矩阵$F$：$F=K_2^{-T}[t]_{\times}RK_{1}^{-1}$，然后我们就可以有如下结论：

基础矩阵有与本质矩阵类似的性质，如下：

  1. 极线分别是：$l_1=Fx_1$和$l_2=F^Tx_2$;
  2. $Fe_1=0$与$F^Te_2=e_2^TF=0$;
  3. $F$是奇异的，秩为2;
  4. $F$有7个自由度(尺度任意，$det(F)=0$)。

估计基础矩阵：归一化八点算法

$F$有7个自由度，理论上7个点就可以求解了，但这样做的话解是非线性的，很麻烦，所以这里用8个点，俗称“八点算法”。\
现假设一个三维点在两成像平面上的观测点分别为：$[x’,y’,1]$和$[x,y,1]$，按照上面的结论我们有：

展开的话即是：

简写成：

由于$f$不能为0，所以添加一个约束：$||f||=1$，这，又是带约束的齐次方程，正经8个点的话直接算，但一般我们会用多于8个点去估计，以减少误差，这时候就可以用SVD分解，相关计算看相机那篇，在这。\
但是在计算之前我们不能忘了数值稳定性，也就是说方程组的系数应该在同一数量级，比如像素是$1E6$，也就是说要预处理，不然会由于数值差异很大导致最后结果精度很低。方法过程如下：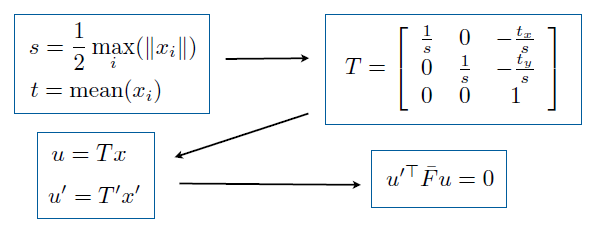
之后就可以求解了。
但用这种方法算出来的还不是我们要求的基础矩阵，因为基础矩阵的秩应该是2，而这种方法算出来的矩阵秩通常为3，即满秩。\
要解决这个问题也简单(且粗暴)，加入在上面我们求出来的满秩“基础矩阵”为 $\widetilde{F}$，我们对其再做一次SVD分解：

令：

接着回构：

由于上面我们对坐标进行了处理，最后一步把$\overline{F}$返回去：

用这种奇异值置零的方法我们可以保证求出的$F$满足在约束 $det(F)=0$ 的情况下最小化 $||F-\widetilde{F}||_F$\
至此求解就结束了。\
上述过程可以用下面这张图总结：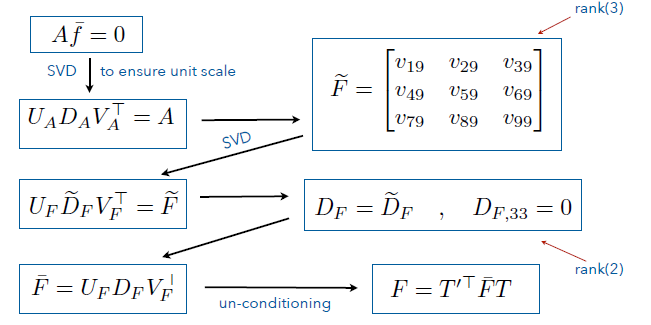

参考

【1】 https://www.youtube.com/watch?v=BKVEvj9F_H4&list=LL&index=42

------ 本文结束------