引入

相机模型化的话，说白了就是一个函数，把一个三维场景转化为二维图像。这里主要是介绍基本相机模型，世界、相机、图像坐标系之间的转换以及相机的标定。

相机模型

这里用最简单也是最广泛的针孔相机模型，单目的，也就是下面这个：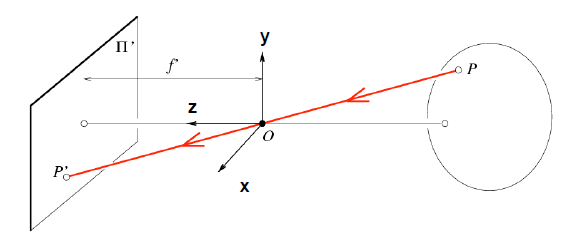
从3D到2D的转换中我们遗失了角度以及距离信息。\
假设点$P$的三维坐标是$[x,y,z]$，其对应图像坐标为$[x^,,y^,]$，有如下关系：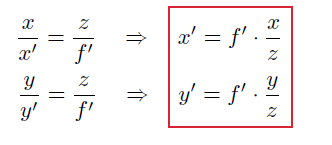
（就是简单的相似三角形）\
也就是说:

$(x,y,z) \rightarrow (f'\frac{x}{z},f'\frac{y}{z})$

用齐次坐标表示的话为：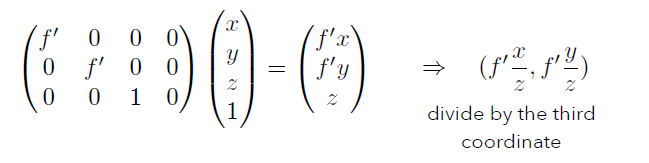
在很多地方左边的那个等式会写成这样子：

$\begin{pmatrix} f'&0&0&0\\ 0&f'&0&0\\ 0&0&1&0 \end{pmatrix} \begin{pmatrix} x\\ y\\ z\\ 1 \end{pmatrix} =z \begin{pmatrix} f'\frac{x}{z}\\ f'\frac{y}{z}\\ 1 \end{pmatrix}$

虽然看上去只是把系数提出来而已，但表达的意思却多了一个：对于同一个图像坐标，其三维坐标有无数种可能，只要在投影线上就行。这是引进齐次坐标的一个很大的特点。

坐标系转变

上面那种情况是最简单的，但一般来说，相机在世界坐标系中的位置是不定的，所以要在中间引入一个新的坐标系————相机坐标系，又叫归一化坐标系。\
所以这里要用到三个坐标系，分别为：世界坐标系，相机坐标系和图像坐标系，它们的转变过程如下：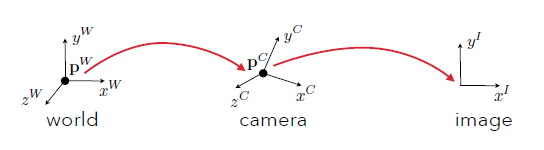
也就是：

首先将世界坐标转为相机坐标\
然后将相机坐标转为图像坐标

世界坐标到相机坐标

(这个过程也就是归一化的过程)\
相机坐标与世界坐标是旋转加平移的关系，即是如下：

$\widetilde{x}^C=R(\widetilde{x}^W-\widetilde{c})$

其中：$\widetilde{c}$是相机中心在世界坐标系中的位置。\
写成齐次形式的话就是：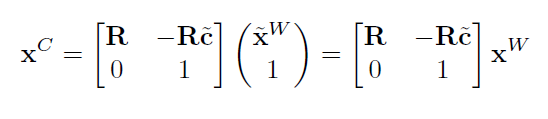
这是一种线性变换的形式，这时候维度还没有遗失\
这个转换矩阵写简洁一点即是：

$x^C= \begin{bmatrix} R&t\\ 0&1 \end{bmatrix} x^W$

其中$t=-R\widetilde{c}$

相机坐标到图像坐标

这里先给三个定义：

主轴(Principal axis)：从相机中心垂直于图像平面的线；\

归一化(相机)坐标系(Normalized (camera) coordinate system)：以相机中心为原点，z轴为主轴的坐标系\

主点(Principal point)：主轴与图像平面相交的点(归一化坐标系的原点）

即是下图这样：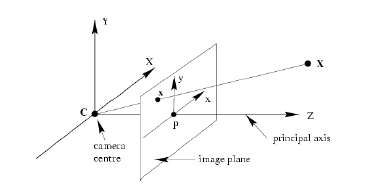

相机坐标系的原点在主点上，而图像坐标系的原点在角落(一般是左上角)，也就是说，两个坐标系存在着偏移量，以图像坐标系为参考的话，该偏移量为$(p_x,p_y)$。\
将最上面那个投影转换写下来，对于三维坐标点$(X,Y,Z)$，其图像坐标为$(f\frac{X}{Z},f\frac{Y}{Z})$，即：

$\begin{pmatrix} f&0&0&0\\ 0&f&0&0\\ 0&0&1&0 \end{pmatrix} \begin{pmatrix} X\\ Y\\ Z\\ 1 \end{pmatrix} = \begin{pmatrix} fX\\ fY\\ Z \end{pmatrix}$

写成紧凑一些的形式为：

$x^I=K\cdot [I|0]\cdot x^C=K\cdot \widetilde{x}^C$

其中：

$K=diag\left\{f,f,1\right\}$

(注意，这里有个非齐次向齐次转换的计算)\
然后考虑这个中心偏移量，即对于三维坐标$(X,Y,Z)$，其图像坐标应为$f\frac{X}{Z}+p_x,f\frac{Y}{Z}+p_y$，写成矩阵计算形式如下：

$\begin{pmatrix} f&0&p_x&0\\ 0&f&p_y&0\\ 0&0&1&0 \end{pmatrix} \begin{pmatrix} X\\ Y\\ Z\\ 1 \end{pmatrix} = \begin{pmatrix} fX+Zp_x\\ fY+Zp_y\\ Z \end{pmatrix}$

这里对应的的$K$为标定矩阵(calibration matrix)，即：

$K= \begin{pmatrix} f&0&p_x\\ 0&f&p_y\\ 0&0&1 \end{pmatrix}$

也就是输入一个归一化的世界坐标，通过矩阵$K$可以得到其对应的图像坐标。\
但是这里还有一个问题，就是说对于世界坐标系，我们用的单位一般会是“米”，“厘米”，“英寸”之类的，但在图像坐标系中我们统一使用“像素”为单位，所以这还需要一个转换过程：

假设在水平方向上以某一单位(m,mm,inch,…)为基准共有$m_x$个像素，在垂直方向上有$m_y$个像素。

就有如下关系：

$K= \begin{pmatrix} m_x&0&0\\ 0&m_y&0\\ 0&0&1 \end{pmatrix} \begin{pmatrix} f&0&p_x\\ 0&f&p_y\\ 0&0&1 \end{pmatrix} = \begin{pmatrix} \alpha_x&0&\beta_x\\ 0&\alpha_y&\beta_y\\ 0&0&1 \end{pmatrix}$

以上这些就是相机的主要内参数，包括有：

主点坐标;\

焦距;\

像素放大系数;\

对于非矩形像素，还有偏斜系数(Skew)，这里不讨论。\

常见的还有畸变参数，这个是为了补充内参数的，下面会讨论。\
这些参数是相机在出厂时就设定好的，一般不会轻易改变。

总结

用一张图简单总结下：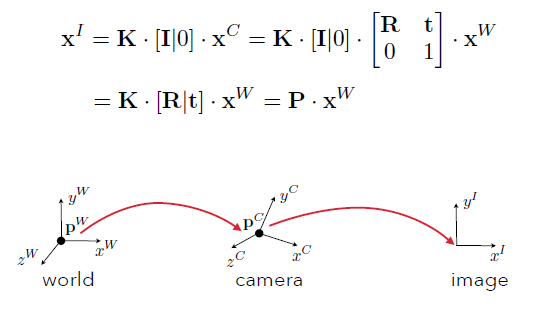
这里的矩阵$P$是投影矩阵，即是给一个齐次世界坐标，通过矩阵$P$，可以得到对应的齐次图像坐标，其中$K\in R^{3\times 3}$，$P\in R^{3\times 4}$。

正投影模型

关于这个简单说一下就好，正投影，也就是平行投影，形式如下：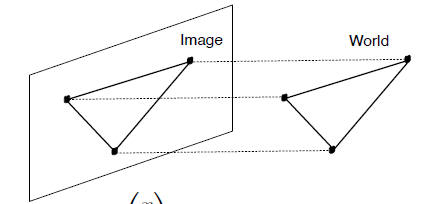
其投影矩阵为：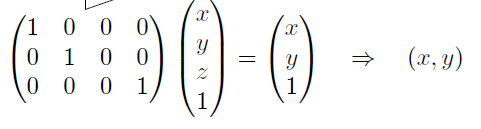

相机标定

相机标定就是根据某些方法确定出相机的内参数和畸变参数。

不考虑畸变

先假设我们有三维坐标点$X_i$，以及对应的图像坐标点$x_i$，都是齐次的，现在想要估计投影矩阵$P$。\
由于共线性，有如下关系：

$\lambda x_i=PX_i$

即：

$\lambda \begin{pmatrix} x_i\\ y_i\\ 1 \end{pmatrix}= \begin{bmatrix} p_1^T\\ p_2^T\\ p_3^T \end{bmatrix}X_i$

这里$p_j^T$表示矩阵$P$的第$j$行。\
用叉积：

$x_i \times PX_i=0$

即：

$\begin{bmatrix} y_ip_3^TX_i-p_2^TX_i\\ p_1^TX_i-x_ip_3^TX_i\\ x_ip_2^TX_i-y_ip_1^TX_i \end{bmatrix}=0$

写成矩阵乘积形式为：

$\begin{bmatrix} 0&-X_i^T&y_iX_i^T\\ X_i^T&0&-x_iX_i^T\\ -y_iX_i^T&x_iX_i^T&0 \end{bmatrix} \begin{pmatrix} p_1\\ p_2\\ p_3 \end{pmatrix}=0$

这个矩阵$P$虽然有12个参数，但由于尺度是随意的，所以实际只要考虑11个自由度就行，然后由于上面那个矩阵等式只提供了两个线性独立等式(因为秩为2)，所以为了求解矩阵$P$，我们最少需要6个 3D/2D 对应点。如果我们有多于6个数据对的话，那就更好了，可以用最小二乘法估计。\
假设我们现在有很多个数据对，根据上面的方法写成如下形式：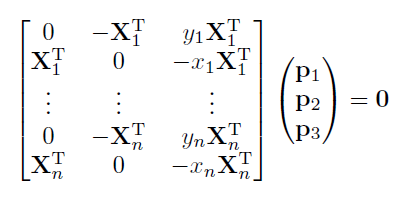
简单记为：

$Ap=0$

由于当$p=0$时虽然符合方程，但明显不是我们想要的，要排除，所以加个约束：$||p||=1$，也就是如下齐次最小二乘形式：

$Ap=0\quad s.t. \quad ||p||=1$

先说解法步骤：

进行SVD分解：$A=USV^T$

假设奇异值是排好序了的，即$S=diag(s_1,…,s_{12}),s_{i+1}\leq s_i$

取最后一个右奇异值向量，此时$p=v_{12}$

为什么是这样？下面简单说明。

齐次最小二乘：简介

现假设向量$p\in R^n$满足：

$Ap=0$

其中$A\in R^{m\times n}$且$0\in R^m$，进一步假设$m\geq n$且$rank(A)=n$。\
由于$A$是测量矩阵，就难免有噪音，所以我们会最小化下面这个：

$||Ap||^2$

为了避免$p=0$这个解，我们在这里加个约束$||p||=1$，也就是说现在我们的问题变为：\

在约束$||p||=1$的条件下，寻找$p$，使得$||Ap||^2$最小。

现在开始解这个问题。\
首先我们改写这个约束条件为：$1-p^Tp=0$，然后用拉格朗日乘子：

$\frac{\partial}{\partial p}(p^TA^TA^Tp+\lambda (1-p^Tp))=0$

即：

$2A^TAp-2\lambda p=0 \quad \rightarrow \quad (A^TA)p=\lambda p$

这里$p$是$(A^TA)$的特征向量，$\lambda$是特征值。\
这就引出了特征值和特征向量了，但现在还有个问题，我们要选哪个特征值/向量？\
回到我们原来的问题，我们要最小化如下的量：

$||Ap||^2=p^TA^TAp$

用约束$||p||=1$改写一下如下：

$||Ap||^2=p^T\lambda p=\lambda$

这就出来了，我们要选的$p$就是$A^TA$最小特征值对应的特征向量。

然后继续，毕竟上面我们的对象是$A^TA$，不是$A$，现在要引进SVD分解。

齐次最小二乘：SVD

SVD，即是奇异值分解，全称为singular value decomposition，表示成如下形式：

$A=USV^T$

其中$U\in R^{m\times n}$，$V\in R^{n\times n}$是正交的(即是逆等于转置，行列式绝对值为1的矩阵)，$S\in R^{n\times n}$是对角矩阵，且值沿对角线递减。\
现在我们有：

$A^TA=(USV^T)^TUSV^T=VS^TU^TUSV^T=VS^2V^T$

上面这个式子就是一个特征值分解(正交性)，所以我们可以看到：

$A^TA$的特征向量就是$A$的右奇异向量；

$A^TA$的特征值是$A$奇异值的平方。

所以，要找$A^TA$的最小特征值，就是要计算$A$的最右边的奇异向量。\
至此就回答完上面的问题了。\
关于SVD分解，详细的可以参看这篇。

通过$P$求$K$

至此我们就求出了投影矩阵$P$，它包含了相机的外参和内参，但相机的标定只要求内参，所以我们要继续往下做。\
这里矩阵$P$是一个$3\times 4$的矩阵，我们把它按如下方式分解：

$P=[M|m]=[KR|-KR\widetilde{c}]$

这里矩阵$M\in R^{3\times 3},m\in R^{3\times 1}$，然后将矩阵$M$进行QR分解成一个上三角矩阵$K$和一个正交的矩阵$R$，这里的$K$就是我们要的标定矩阵，$R$是旋转矩阵。最后，通过SVD找到c作为P的零空间。\
至此，这种不考虑畸变的标定就结束了。

考虑畸变参数

上面是特殊情况，一般在现实中我们是不能忽略畸变参数的，在进行标定前，先对畸变参数作简要说明。\

畸变参数

根据畸变的方式不同畸变参数可分为两部分，径向畸变和切向畸变(还有其他的比如薄透镜畸变，这里不考虑)。

径向畸变

径向畸变是由于透镜形状的制造工艺导致。且越向透镜边缘移动径向畸变越严重。\
比如说这是我们正常的图像：
其中的像素点坐标我们用极坐标来表示，为$(r,\theta)$，径向畸变的话，就是$r$的缩放，其又分为两种，分别为桶形畸变和枕形畸变，如下：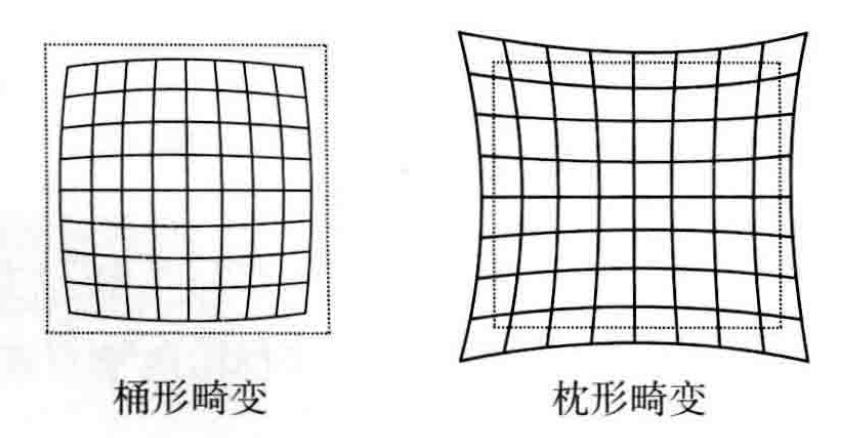
其中桶形畸变大都发生在使用广角镜头或使用变焦镜头的广角端时，枕形畸变则是使用长焦镜头或使用变焦镜头的长焦端时发生。\
用数学形式表示的话，我们先假定归一化平面上有一点$p$，坐标为$[x,y]^T$，对应的极坐标形式为$[r,\theta]^T$，其中$r$表示与坐标系原点的距离，$\theta$表示与水平轴的夹角。径向畸变的话就是$r$发生了变化，畸变后的坐标可表示为：

$x_{distorted}=x(1+k_1r^2+k_2r^4+k_3r^6)$ $y_{distorted}=y(1+k_1r^2+k_2r^4+k_3r^6)$

这里的$k_1,k_2,k_3$即是径向畸变参数。\
这里的多项式不一定非得是这几个，可以多写几项或少些几项，看自己需求吧，不过大都用这几个表示。\

切向畸变

切向畸变是由于透镜本身与相机传感器平面（成像平面）或图像平面不平行而产生的，其畸变来源示意图如下：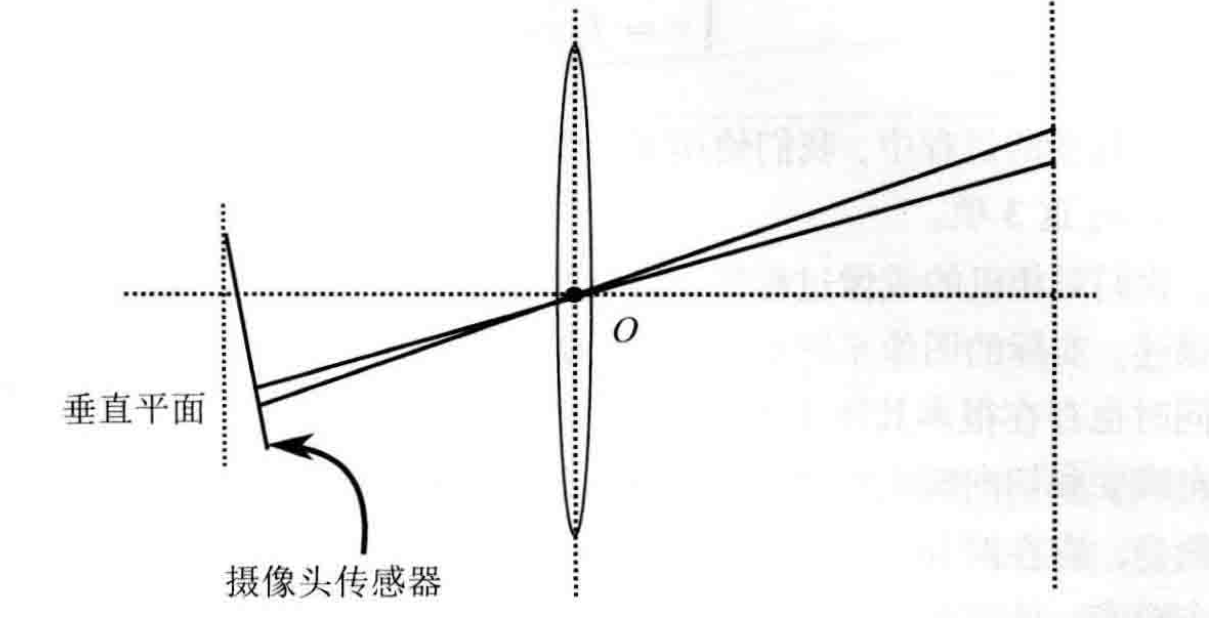
同样可用数学表示如下：

$x_{distorted}=x+2p_1xy+p_2(r^2+2x^2)$ $y_{distorted}=y+p_1(r^2+2y^2)+2P_2xy$

这里的$p_1,p_2$就是切向畸变参数。

求解畸变参数

首先，根据上面两类畸变可知，一个畸变后的坐标应该是这样的：

$x_{distorted}=x(1+k_1r^2+k_2r^4+k_3r^6)+2p_1xy+p_2(r^2+2x^2)$ $y_{distorted}=y(1+k_1r^2+k_2r^4+k_3r^6)+p_1(r^2+2y^2)+2P_2xy$

这里涉及到5个畸变参数，分别为：$k_1,k_2,k_3,p_1,p_2$。\
畸变的话不能直接求解，但可以用优化的思想，目标函数选用最小化重投影误差，也就是将空间坐标点按照估计的投影方程投影到图像上，得到像素估计值，使该值与实际观测值之间的误差最小。\
其中变量初始值设为：畸变参数为0，其余参数用上面无畸变标定的方法的结果。\
注意，这里的优化变量不只是畸变参数，还有其余内参。\
至于其中的优化细节，一大堆公式还没看，留着以后吧。\
其实直接用OpenCV或者Matlab就可以弄出来了，尤其是Matlab，真-傻瓜式操作，不过还是得知道这些内部算法的。这个优化细节，以后有心情的话看完再补充了。

附

关于坐标系的投影变换，可以看这个，有直接的例子。

参考

【1】视觉SLAM 14讲\
【2】 https://shartoo.github.io/2016/10/25/SVD-decomponent/ \
【3】 https://www.qinxing.xyz/posts/b7ea425d/ \
【4】 https://zhuanlan.zhihu.com/p/24651968 \
【5】 https://zhuanlan.zhihu.com/p/87334006

SuperZLW's Blog

相机模型与标定

引入