SuperZLW's Blog

我很笨，但是我不懒

0%

RANSAC算法

发表于 分类于 Valine：

引入

当我们有一组数据需要拟合模型的时候，最简单的是用最小二乘法，又叫线性回归去拟合，然而这种方法是用所有数据去拟合，如果所有数据都是跟模型有关的话，那效果应该还行，但如果我们的数据集有很多数据是属于”outliers”的话，效果就会很差，这时候可以用这篇的这个算法：RANSAC算法。

简介

用这个算法的前提是，我们假设：我们的数据是由”inliers”和”outliers”组成的，并且这个”outliers”还不少(少的话也可以用，看有没有必要而已)，而且我们需要知道这个”inliers”大概占了多少，这个量属于先验，需要事先知道的。实际实现算法时我们还需要确定的有以下几个参数

  1. 得到正确模型的概率：字面意思，就是说有多大概率能得到正确模型，即是选出的用于拟合模型的点都是”inliers”，这个参数是用来算最大迭代次数的;
  2. 迭代次数：这个可以根据上面的概率来算，下面会解释;
  3. 模型参数的数目：也就是说我们要知道拟合的这个模型我们需要多少参数，比如直线是2个，Homography矩阵是4个;
  4. 阈值：即是判断点属于”inliers”还是”outliers”。

计算迭代次数

比如说，所有数据中”inliers”占的比重为$w$，拟合模型需要$d$个参数，也就是说$d$个数据点，那么我们从数据中选出$d$个数据都是”inliers”的概率是: $w^d$，至少有一个”outliers”的概率是 $(1-w^d)$，$k$次循环每次都至少有一个”outliers”的概率是：

那么选到正确$d$个”inliers”的概率是：

求得：

代码

(因为这个算法不难，这个代码也是随手写的，所以这个代码风格很不好，参数命名也不太行。所以这东西，大概看看就好)。\
这里是用最简单的直线拟合，有40个”inliers”，都添加了高斯噪音，并且有60个随机的”outliers”，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
import matplotlib.pyplot as plt
import numpy as np

def Gauss_noise(data):
    """
        data: ndarray, (2,n)
    """
    noise_x = np.random.normal(0,1,len(data[0]))
    noise_y = np.random.normal(0,1,len(data[1]))
    data[1] += noise_y
    data[0] += noise_x
    return data

def real_model(x):
    a = 4
    b = 6.9
    y = a * x + b
    return y

def outliers(nums = 60):
    down = 0
    up = 40
    outliers = np.random.rand(2, nums)*60
    return outliers


inliers_nums = 40
outliers_nums = 60
x = np.linspace(0,20,inliers_nums).reshape(1,-1)
y = real_model(x)
inliers = np.concatenate((x,y), axis=0)
inliers = Gauss_noise(inliers)
outliers = outliers(outliers_nums)

data = np.concatenate((inliers, outliers),axis=1)

data_nums = len(data[0])
    
estimate_a = 0.
estimate_b = 0.

accuracy = 0.99
error = 0.8
current_inliers = 0
curr_iter = 0

accept_nums = int(0.4 * data_nums)

max_iter = np.log(1 - accuracy) / np.log(1 - (inliers_nums / data_nums)**2)
while current_inliers < accept_nums and curr_iter < max_iter:
    curr_iter += 1
    ids = np.random.choice(range(data_nums), 2, replace = False)
    x_1 = data[0,ids[0]]
    x_2 = data[0,ids[1]]
    y_1 = data[1,ids[0]]
    y_2 = data[1,ids[1]]

    a = (y_2 - y_1) / (x_2 - x_1)
    b = y_1 - a * x_1

    tmp_inliers = 0
    for i in range(data_nums):
        y = a * data[0,i] + b
        if np.abs(data[1,i] - y) < error:
            tmp_inliers += 1

    if tmp_inliers >= current_inliers:
        estimate_a = a
        estimate_b = b
        current_inliers = tmp_inliers

plt.figure()
plt.scatter(data[0],data[1])
plt.plot(data[0,:40], estimate_a * data[0,:40] + estimate_b, color='r')
plt.show()

效果如下：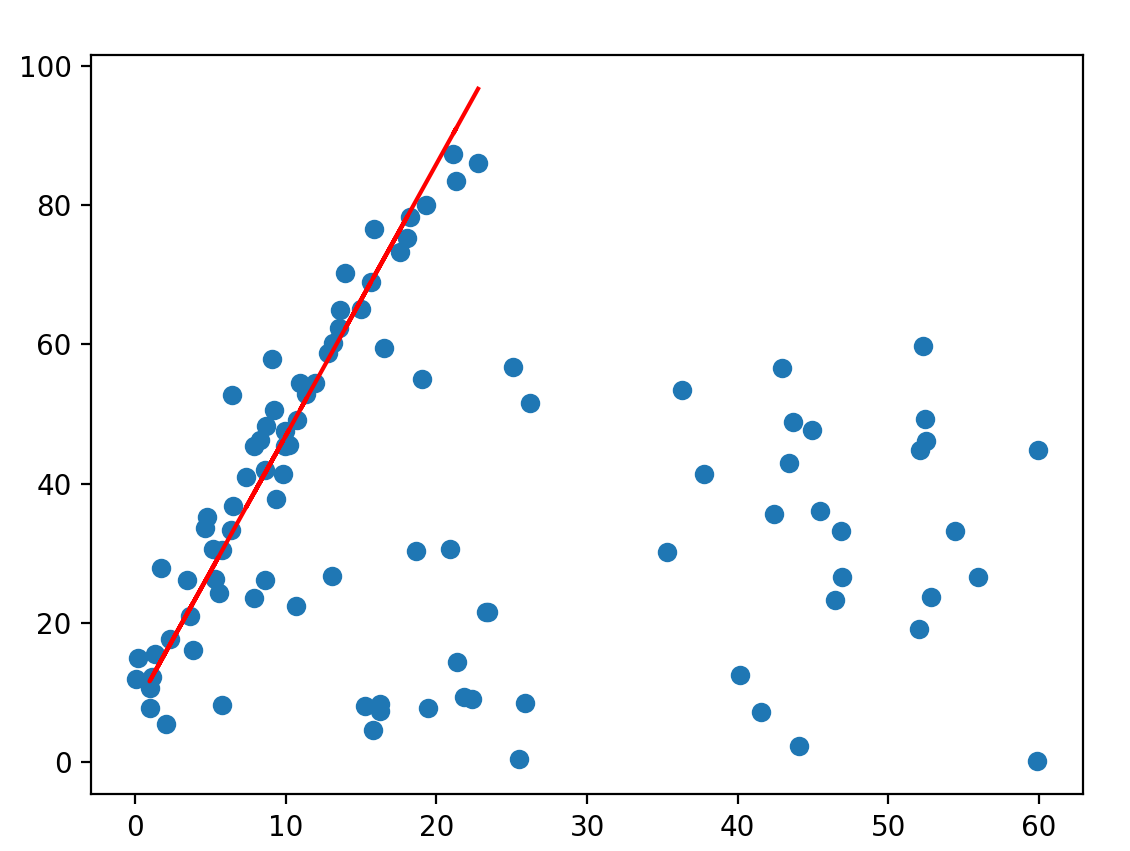

再提一个，既然这个算法可以用来区分”inliers”和”outliers”，那要是我先用这个算法把”inliers”分出来，然后用线性回归，效果会不会更好？\
然而试验发现，好是有好那么一点点吧，主要是那个bias更接近了，但区别真的不大，代码写得很乱就不贴了，反正貌似也没啥意义。。。

------ 本文结束------