引入
拟合优度检验是用来检测提出的模型与数据是否一致,这在数据科学领域很重要,因为通过这种检测可以知道:
- 数据是否符合我们提出的假设(比如高斯性);\
- 两个数据集的分布是否可以假定为相同。
一般来说:
- 离散分布对应于Chi-square test ;\
- 连续分布对应于Kolmogorov Smirnov。
Chi-square test
这个就是经常能听到的卡方检测,卡方检测一般有两种,分别为拟合度的卡方检验和卡方独立性检验,这里重点介绍第一种。\
拟合度卡方检测
简单定义的话,就是使用样本数据检验总体分布形态或者比例的假说,或者说得再清楚一点,检验该样本的分布比例与总体分布比例的拟合程度。\
拟合度卡方检测又分为如下两种情况:\
case 1: 所有参数都是确定的
由于这是检验分布比例的,所以零假设和备选假设可以写成这样:
- $H_0$: $P\left\{ Y=i\right\}=p_i$ vs $H_1$: $P\left\{ Y=i\right\}\neq p_i$, $i\in$ {$k$ discrete outcomes}。\
定义如下变量:\
$X_i$ 为输出结果 $i$ 在 $n$ 次重复试验中出现的次数,单看结果 $i$ 的话,可以看成是二项分布,所以有 $E[X_i]=np_i$。\
检测统计量为:
当次数 $n$ 很大,且零假设成立时,$T$ 可近似看作是 $k-1$ 个自由度的卡方分布,就可以查阅卡方表进行比较了。\
最后根据设置的 $\alpha$ 值,当 $T \geq \chi_{\alpha,k-1}^2$ 时,拒绝零假设,否则接受。\
一个例子
在一个试验中共有6个可能的输出分别是 $a,b,c,d,e,f$,现假设其出现概率分别为:0.1,0.1,0.05,0.4,0.2,0.15,试验重复40次所得到的各结果频数分别是:3,3,5,18,4,7。问:一开始那个频率假设是否合理?\
零假设$H_0$:\
计算统计量\
将 $n=40$,6个$p_i$代入 $T=\sum_i\frac{(x_i-np_i)^2}{np_i}$ 求出 $T=7.416666667$。\
查表\
设$\alpha=0.05$,自由度$df=6-1=5$,查表得: $\chi_{0.05,5}^2=11.070$。\
决策\
由于 $T \leq \chi_{0.05,5}^2$,所以接受零假设。
case 2: 某些参数都是未确定的
与上面$n$和$p_i$都确定的情况不同,这里有些参数是不确定的,需要我们根据其它办法(比如MLE)近似确定。\
假设我们有 $m$ 个未指定的参数,需要我们用MLE来确定,比如说泊松分布 $Y\sim Pois(\lambda)$ 的均值的MLE估计为: $\hat{\lambda}=\frac{1}{n}\sum_{j=1}^ny_j$;\
测试统计量为:
这里的$\hat{p}_i$是估计参数。\
比如说泊松分布的$pmf$为: $P(Y=i)=\frac{e^{-\lambda}\lambda^i}{i!}$\
将数据分为$k$组,每组进行分布统计。\
若试验次数$n$足够大且零假设为真,则$T$近似为卡方分布,自由度为 $k-1-m$。\
对于设定值$\alpha$,若 $T \geq \chi_{\alpha,k-1-m}^2$,则拒绝零假设,否则接受。
一个例子
我们有下面30个数据,表明30周里每周车祸发生的次数,现在需要验证一周事故发生次数服从泊松分布。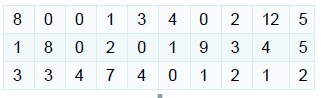
我们将数据分成如下5组:
步骤1\
首先我们对数据根据分组进行统计,结果如下: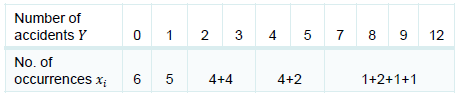
步骤2\
计算估计参数 $\hat{\lambda}$;\
根据上面泊松分布的MLE计算,这个参数就是数据的均值了,等于:$\hat{\lambda}=3.167$;\
步骤3\
根据求出的估计参数,代入泊松分布的 $pmf$ 中,计算各个组的概率:
步骤4\
计算验证统计量:
步骤5\
查卡方表,根据 $\alpha=0.05$,自由度$df=k-1-m=5-1-1=3$ 查得:$\chi_{0.05,3}^2=7.815$。\
步骤6\
决策,由于$21.99\geq 7.815$,所以拒绝零假设,一周事故频数不服从泊松分布。\
卡方独立性检验
这里只是简单介绍怎么用这个检验,要具体推导的话看这里。\
卡方独立性检验是为了检验两个变量是否独立,比如说性别与考试通过率是否独立,或者会不会说英语与收到的offer是否独立等。\
这里直接用链接里的这个例子,两个变量分别是性别与分期与否。\
观测值如下:
| 分期 | 不分期 | ||
|---|---|---|---|
| 男 | 90 | 110 | 200 |
| 女 | 30 | 70 | 100 |
| 120 | 180 |
这里的 90,110,30,70分别用$o_1,o_2,o_3,o_4$表示。\
做零假设:两变量独立。\
根据这个零假设,我们期望的值应该是(就是比例相同):
| 分期 | 不分期 | ||
|---|---|---|---|
| 男 | 80 | 120 | 200 |
| 女 | 40 | 60 | 100 |
| 120 | 180 |
这里的80,120,40,60分别用$e_1,e_2,e_3,e_4$表示。\
计算卡方统计量:
查表验证。
Kolmogorov Smirnov
这种检测方法是基本思路就是,比较理论的经验累积分布与观测的经验累积分布,求出最大偏离值,然后判断这种偏离值是不是偶然出现的。\
比如说现在有一个连续分布的样本数据:$y_1,…,y_n$。\
我们做出零假设:$F$ 是总体连续分布。\
现在验证这个零假设,有两种方法:
- 将该分布分成不同区间,然后用上面的卡方检测;\
- 用 K-S 检验。
举个例子,现在有$n=5$个数据:$y_1,y_2,y_3,y_4,y_5$,根据这5个数据得出的经验累积函数为:
零假设对应的函数为$F$,画图如下: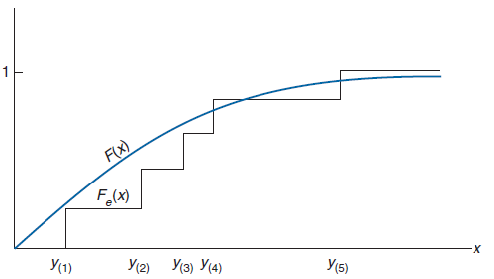
如果零假设成立,则$F_e(x)$应该很接近于$F(x)$。\
K-S 检测的统计量为(就是最大距离):
下图是sample test: Use the One sample Kolmogorov Smirnov table: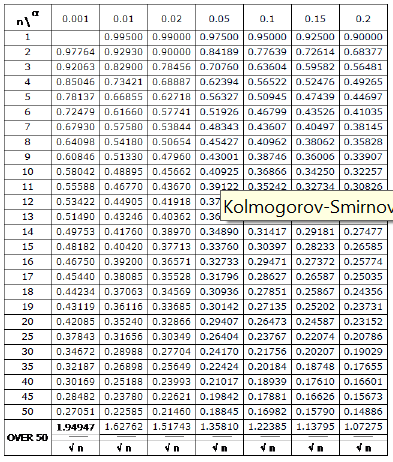
(至于sample tests use the two sample Kolmorogov Smirnov table ,在这里)\
根据$\alpha$和$n$就可以读出临界值,两者比较,当最大值小于临界值时,接受零假设,否则拒绝。\
简单说一下双样本的
双样本检测也差不多,只是多了一组样本,表也多了一个维度,计算距离也不太一样,就,样本数据很大时,距离公式为:
系数$c(\alpha)$为:
总结
直接附图了这里 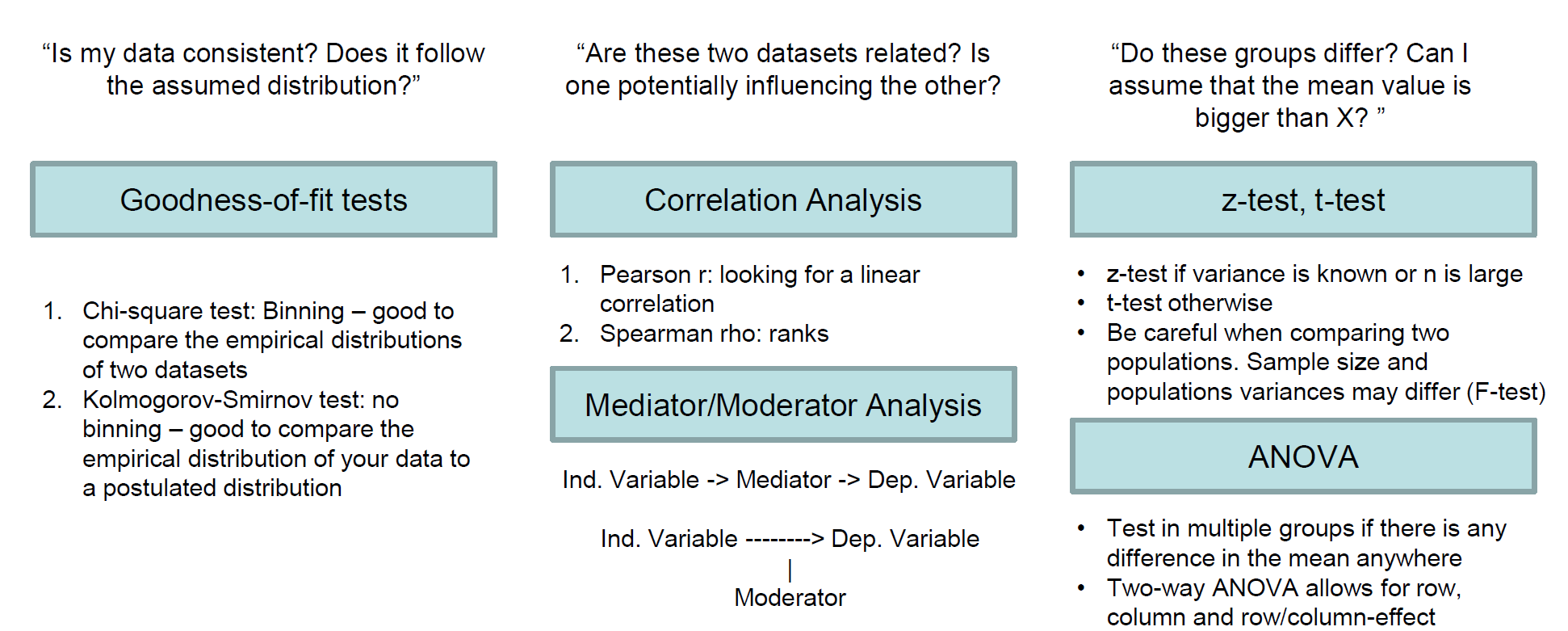
参考
【1】:https://zhuanlan.zhihu.com/p/131286213
【2】:https://qinqianshan.com/math/significance_test/kolmogorovsmirnov/