引入

目前关于光流一共学过三种方法，分别为LK光流，HS光流以及概率法，一步一步来吧，这里先讲LK光流，之后如果学了其它方法再来更新。

光流

光流（optical flow）是指空间运动物体在观测平面上的像素运动的瞬时速度。一般用图像序列中像素在不同时间上的变化来确定相邻帧之间的相关关系，从而计算出相邻帧图像的运动。当相邻帧时间间隔足够短时，我们可以用目标点的位移来代指这个速度。\
简言之：

Optical flow = 2D velocity field describing the apparent motion in the images.

光流场的话，是指图像中所有像素点构成的一种二维瞬时速度场，如下图的例子所示：

光流估计

光流估计即是通过给定的两帧图片，估计它们之间的$u(x,y)$和$v(x,y)$。\
为了计算光流，我们会首先做以下两个假设：

假设1：对于图像中的小区域，尽管它们的位置可能发生变化，但小区域中的图像测量值(例如亮度)保持不变，称为亮度恒定假设。\
假设2：场景中的相邻点通常属于同一表面，因此通常具有相似的3D运动。称为空间连续性假设。

对于假设1，用数学表示的话可以写成如下形式：

$I(x+u(x,y),y+v(x,y),t+1)=I(x,y,t)$

其中$u(x,y)$和$v(x,y)$分别称为水平流位移和垂直流位移。\
计算这个光流最直接的想法是最小化亮度差异，亮度差异可表示为：

$E_{SSD}(u,v)=\sum_{(x,y)\in R}(I(x+u,y+v,t+1)-I(x,y,t))^2$

也就是计算一个区域像素在某一方向的亮度差异。\
再具体一点的话，就是对每个像素，取其邻近区域并尝试所有可能的运动，取一个最小的$SSD$，该方向即为该区域像素的光流方向。\
但这么算的话效率很低，而且把运动空间分散了，这跟现实不太符。\
所以我们希望找到另一个方法来近似。

改进

对于上面那个差异公式，右边第一项可以写为：

$I(x+u,y+v,t+1)=I(x+\Delta_x,y+\Delta_y,t+\Delta_t)$

继续用泰勒级数展开可表示为：

$I(x,y,t)+\Delta_x\frac{\partial}{\partial x}I(x,y,t)+\Delta_y\frac{\partial}{\partial y}I(x,y,t)+\Delta_t\frac{\partial}{\partial t}I(x,y,t)+\epsilon(\Delta_x^2,\Delta_y^2,\Delta_t^2)$

最后一项$\epsilon$是近似误差，当$\Delta_t$足够小时，这个误差近似为0。\
所以上面的SSD近似可写为：

$\begin{split} E_{SSD}(u,v) &\approx \sum_{(x,y)\in R}(I(x,y,t)+u\frac{\partial}{\partial x}I(x,y,t)+v\frac{\partial}{\partial y}I(x,y,t)+\frac{\partial}{\partial t}I(x,y,t)-I(x,y,t))^2\\\\ &= \sum_{(x,y)\in R}(u\frac{\partial}{\partial x}I(x,y,t)+v\frac{\partial}{\partial y}I(x,y,t)+\frac{\partial}{\partial t}I(x,y,t))^2\\\\ &= \sum_{(x,y)\in R}(u\cdot I_x(x,y,t)+v\cdot I_y(x,y,t)+I_t(x,y,t))^2 \end{split}$

这个SSD近似方程相较于更上面的那个差异性方程来说，这个方程对于运动$u,v$是凸的，所以更容易计算，但是，这只适用于小运动的情况。\
当$\Delta_t$足够小趋近于0的时候，我们有下面这个式子：

$u\cdot I_x+v\cdot I_y+I_t=0$

这就是光流约束方程(optical flow constraint equation, OFCE)，也成为线性化亮度恒定约束。\
上面这个约束方程可改写成下面形式：

$\Delta I^Tu=-I_t$

其中:

$u= \begin{pmatrix} u\\v \end{pmatrix} \quad \Delta I= \begin{pmatrix} I_x\\ I_y \end{pmatrix}$

*\
另外，对于这个公式的推导，有些地方会这么写，都一个意思：

$\frac{dI}{dt}=\frac{\partial I}{\partial x}\frac{dx}{dt}+\frac{\partial I}{\partial y}\frac{dy}{dt}+\frac{\partial I}{\partial t}$

当假设每个场景点的图像强度随时间推移而不变时(例如亮度)，则有：

$\frac{dI}{dt}=0$

则：

$u\cdot I_x+v\cdot I_y+I_t=0$

两种推导一个意思。\
*\
用这个约束的话有个问题，也就是下面提到的孔径问题(The Aperture Problem)。

The Aperture Problem

孔径问题(The Aperture Problem)的话，表现为下图这种情况

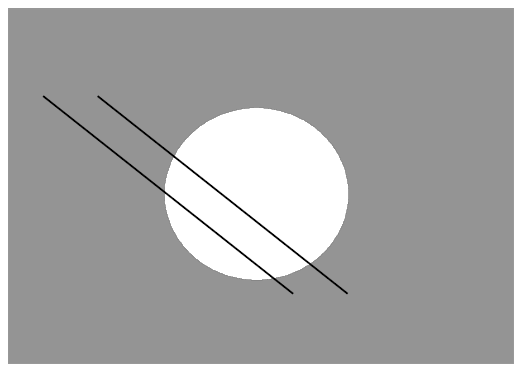
也就是说对于第一幅图，虽然线是往右平移的，但我们的判断却是下面这样：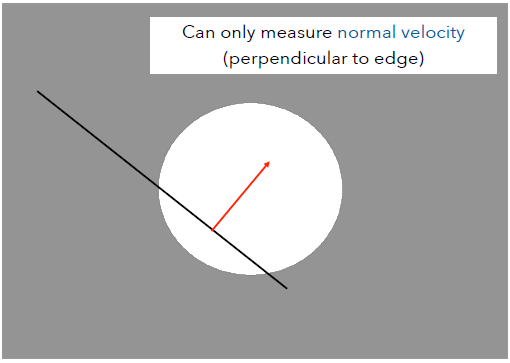
简单解释一下，现假设我们取一个单一的像素点，并得到了下面这个约束方程：

$u\cdot I_x+v\cdot I_y+I_t=0$

画出来的话如下图：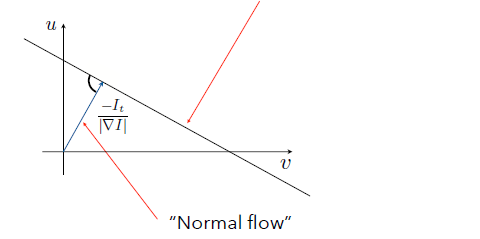
这里有两个未知数，却只有一条线，我们没法确认具体的$u,v$，所以我们就取图中”Normal flow”方向的值(如果还有一条线确定一个交点，那就不用纠结了)。\
再举个例子，如下图：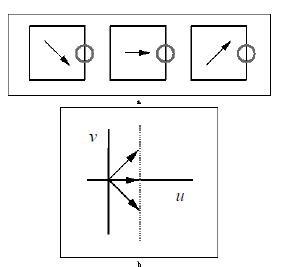
与上面情况类似，对于光圈中观察到的直线的移动，有无数种可能，上图只取其中三种，列出下面这个约束方程：

$u\cdot I_x+v\cdot I_y+I_t=0$

由于我们这种情况下我们只研究垂直方向，也就是中间这种(这是人为定的)，因为其它可能性我们没法研究，除非有先验。也就是说$v$方向没运动，所以我们有：

$u\cdot I_x+0\cdot I_y+I_t=0$

进而：

$u=-\frac{I_t}{I_x}$

现在反过来考虑，由于我们只研究$u$方向，$v$方向没运动的话，即是:$I_y=0$，此时$v$可为任意值。\
这就是常见到的两个结论：

梯度方向的光流是确定的；

但平行于边缘的光流是未知的。

(这部分不太好用文字说明，很多地方直接说“由约束方程直觉上可知”上面两个结论，图也不给，神它喵的“直觉”……)\
这部分知道是怎么回事就行。\
也就是说运动场跟光流不一定一样，举个更简单的例子，理发店门口的颜色柱
其运动场和光流分别是：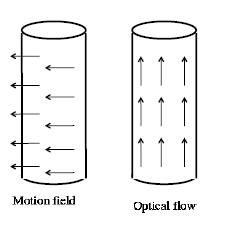

多个约束

上面说到，因为两个未知数一条线所以我们只能估计法线方向的光流，那现在我们找多几个点，就会有下面这种情况：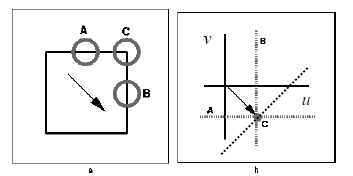
这就确定下来了。我们能这么做是因为上面有了假设2，也就是空间连续性假设，也就是说假设光流在一个区域内是恒定的。\
回到上面那个式子：

$E_{SSD}(u,v) \approx \sum_{(x,y)\in R}(u\cdot I_x(x,y,t)+v\cdot I_y(x,y,t)+I_t(x,y,t))^2$

要计算运动的话这里分别对$u,v$求导并使其为0：

$\frac{\partial}{\partial u}E_{SSD}(u,v) \approx 2\sum_{(x,y)\in R}(u\cdot I_x(x,y,t)+v\cdot I_y(x,y,t)+I_t(x,y,t))I_x(x,y,t)=0$ $\frac{\partial}{\partial v}E_{SSD}(u,v) \approx 2\sum_{(x,y)\in R}(u\cdot I_x(x,y,t)+v\cdot I_y(x,y,t)+I_t(x,y,t))I_y(x,y,t)=0$

即：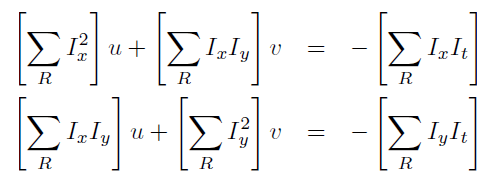
写成矩阵形式：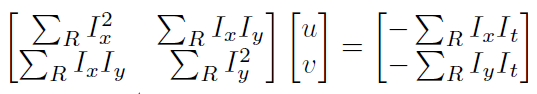
左边第一个矩阵是对称正定矩阵，可逆，它的特征向量给出了局部图像变化的主要方向。特征值则表示其强度。\
此时求个逆光流$u,v$就算出来了。
这种方法就是LK光流法。