引入
记录一种基于α拓展和图像切割技术的图像去噪的方法，作业的其中一题，貌似也没在网上看到相关的东西，觉得挺有意思就记一下。顺便也总结一下其中用到的方法。
Graph Cuts
这里以二元分割为例，即是说 disparity 只取[0, 1]，如下图所示：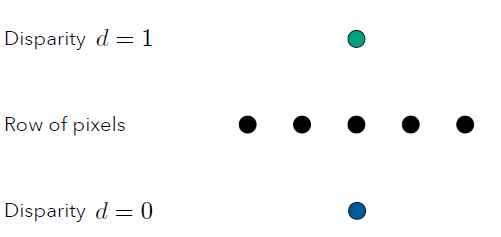
然后现在就要对每个像素进行分类，或者说切割，但我们要怎么判断一个像素属于哪个 disparity 呢，这里就要引入Cost，有两种，第一种如下图：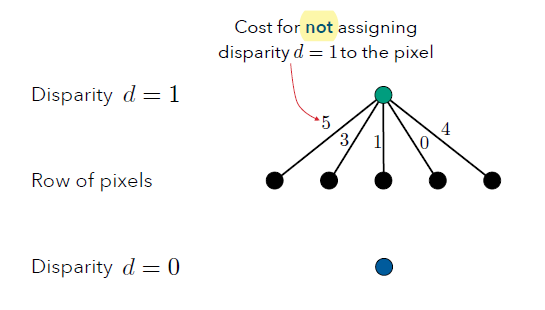
也就是说这里的 5 表示该像素不分配到 $d=1$的Cost，同理，对于下面$d=0$也会有对应的Cost；\
第二种是：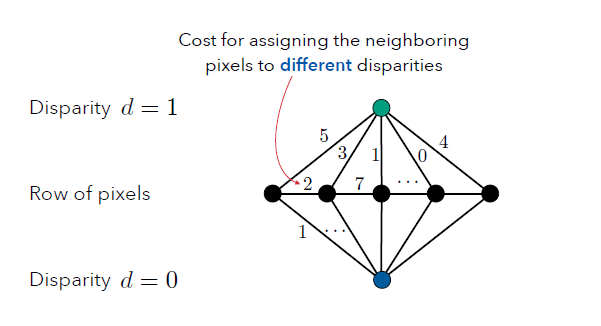
也即是说这里的2表示把相邻像素分配给不同disparity的Cost。\
现在我们要考虑的就是如何把不同的像素归到不同的disparity，这里介绍一种最常用的方法：最大流/最小割法 (max-flow/min-cut)。
最大流/最小割法 (max-flow/min-cut)
最大流
这部分直接去看【参考1】比较好
乍看之下这好像是两种方法，但在这里这两个东西其实本质上是一样的。\
【参考1】其实已经讲得很好了，我这里结合【参考2】再理一遍，至少让我印象深刻一点。\
以水管输送水为例，要从起始点送水到目标点，某一路径最大允许流量应取决于该路径最脆弱那段水管所能承受的最大流量，不然会爆，以下图为例: 
这里只有一条路径，且最小值为2，即是说该路径的最大流为2。\
如果路径多一点的话那就不太好算了，以下图为例：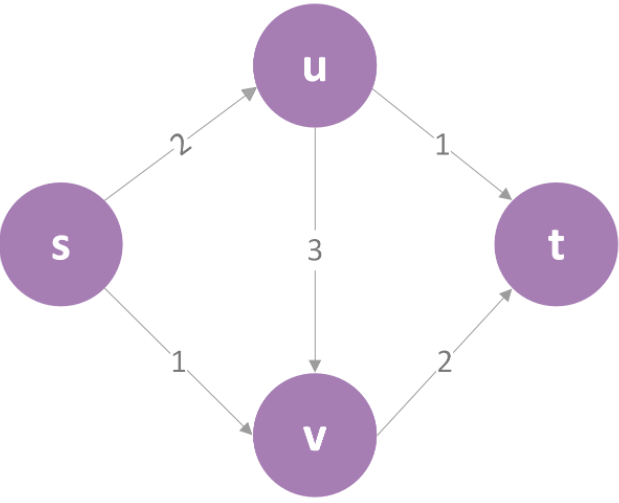
对于路径“s->u->v->t”，最小值为2，即该路径允许的最大流为2，用了流量2后当前状态就变成下图的状态了：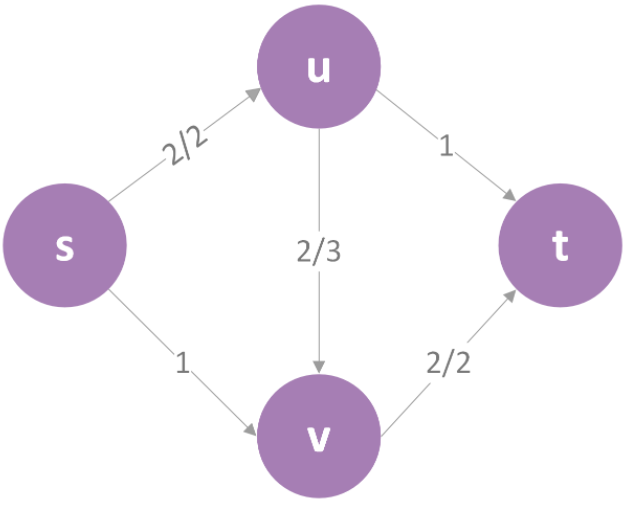
(这里的x/y 表示容量最大为y，现已经用了x。)\
这时候就会发现没路径可走了，并作出判断：该图最大流为2。但显然这种判断是错的，下面这种情况才是对的：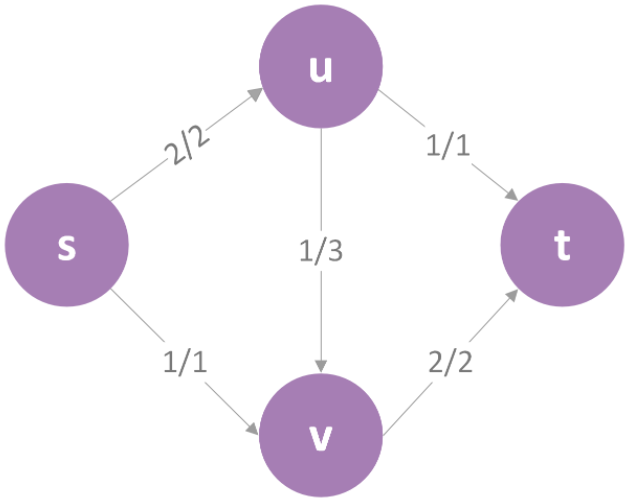
为了得到正确的流量，上面那种简单路径叠加的方法明显是行不通的，这时候就要用residual graph了。
residual graph
这个方法的核心思想就是可以撤销之前的操作，这样就可以考虑得更全面(学过“图”算法的应该很容易理解，但我没学过，只在leetcode上做过广度/深度优先搜索算法题，意思差不多，所以对这部分我只是基本理解，并不全面)。\
当我们选择了路径“s->u->v->t”时，其允许的最大流为2，此时按照这个流量从终点往起点回溯，图如下：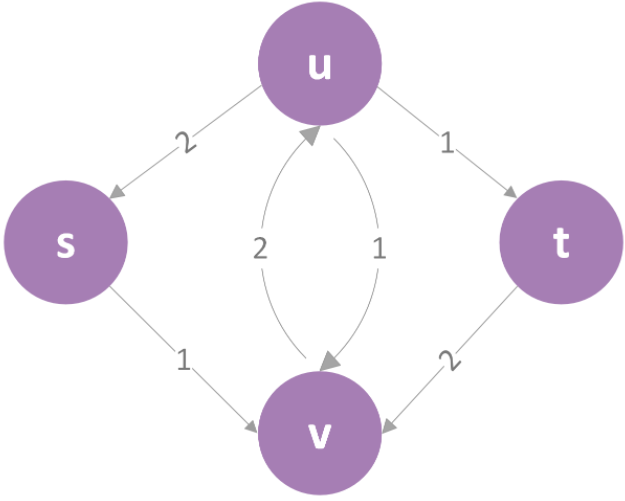
抵消部分如果是0就省略了。\
然后现在在根据这个新图找一条新的路径，比如说“s->v->u->t”，其允许的最大流为1，回溯后又得到一个新图如下：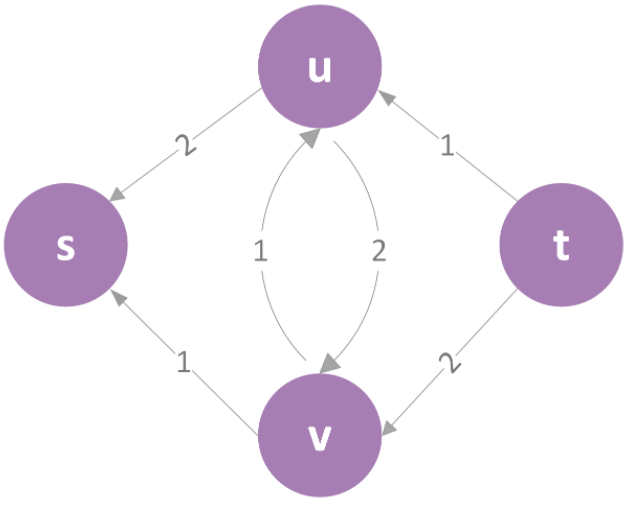
根据这个图我们没办法找到新路径了，所以最大流为2+1=3，这就是最终的结果了。\
最小割
最小割的话就简单说了，即是把不同像素归到不同的disparity，使这种归类所需的能量最小，比如说下面这幅图：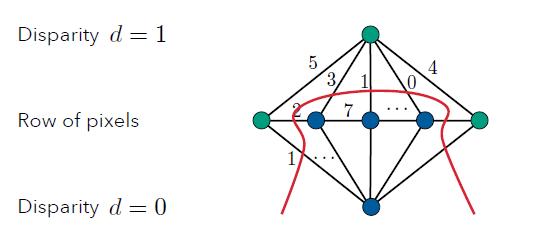
𝝰-expansion
上面的图割法显然只对二分类有用，经常用于分离背景和目标物，但如果要处理多个标签，就要用到𝝰-expansion了。\
这种方法简单说就是迭代地使用图割找到能量(或者对数后验)地局部最优解。\
基本思想是：
- 初始化disparity map，比如全部设0；\
- 以随机顺序反复扫过所有的disparity；\
- 将中间解决方案视为一个disparity level，当前提出的disparity level视为另一个；\
- 解决二进制的图割问题；\
- 重复进行，直到在一次扫描中没有像素被更新为止。
用图表示的话就是：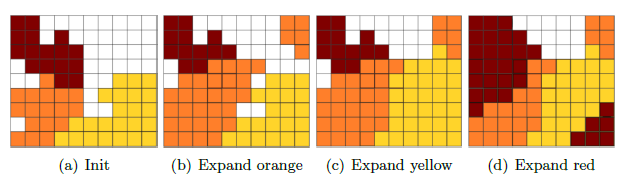
简单解释一下：𝝰-expansion将多标签问题表示成一系列的二元子问题，在每一步里，我们选择一个标签 α 并拓展：对于每个像素，要么保持标签原样，要么用 α 替换。每个子问题都能以全局最优的方式得到解决。 a) 初始标签。 b) 橙色标签扩大：每个标签保持不变或变成橙色。 c) 黄色标签扩大。 d) 红色标签扩大。
作业解释
(作业代码依旧在GitHub里，如果没有，那就是还没整理好)\
𝝰-expansion 提供了一种对具有多个标签的马尔科夫随机网格（MRF）进行推理的方法，将解决方案分解为一系列二进制问题，其中每个问题都可以被精确解决。其主要思想是对每个标签进行迭代，在每次迭代中，所有节点都可以选择保留其当前标签或切换到新标签，如上图所示。\
这里实现一种近似版本的𝝰-expansion，现假设图像被标准差为$\sigma_N$的高斯噪音破坏，并且这个高斯噪音是像素独立的(pixelwise independent)。\
对于尺寸为$H\times W$的图像，放弃一些常数项，我们可以写出一个适当的似然模型：
这里$x,y\in R^{H\times W}$分别是原始图像和被破坏的图像。\
不写下去了，到时候直接在代码里加注释吧。。。