引入

接上一篇的【有参估计】，这篇介绍无参估计，也就是说在这里我们事先不知道数据的模型，而要求数据进行划分，这也是实际中比较常见的情况。

这主要介绍三种无参估计方法，分别是：

1. 直方图（Histograms）
2. 核密度估计（Kernel Density Estimation，KDE）
3. K最邻近法（K-nearest Neighbors，KNN）

直方图（Histograms）

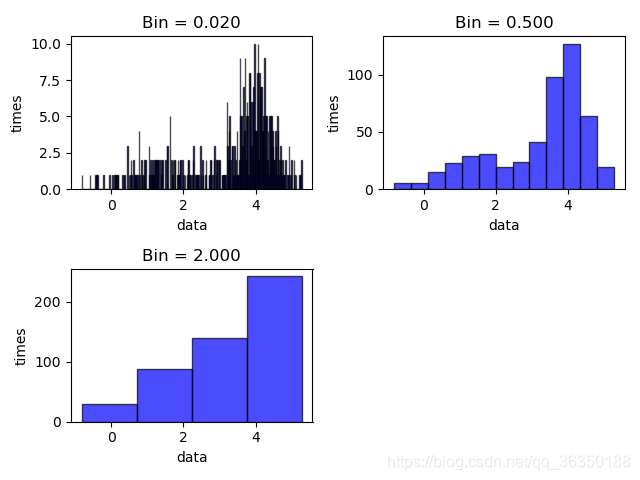
直方图是最简单的一种方法，通过对数据进行统计分类，画出直方图即可，这里需要注意的是直方图中$bin$值的选取。\
对于$bin$值的不同选取可能会有下面三种情况：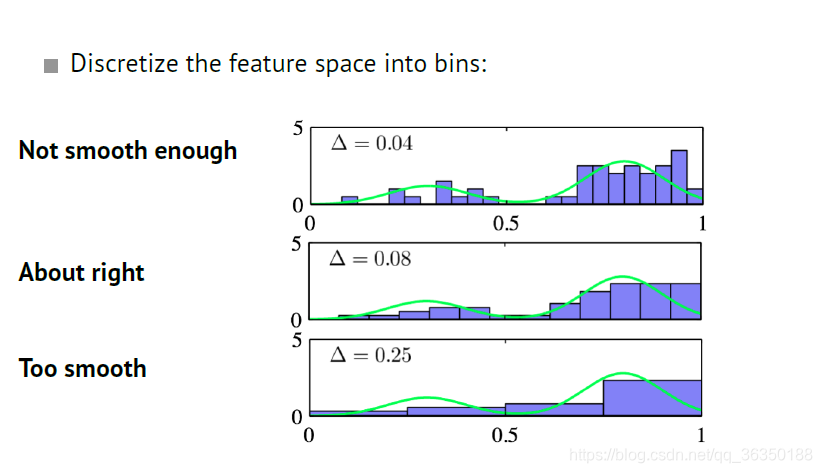

直方图的特点是：

使用非常普遍，没有数据的限制，任何概率密度都可以被任意地近似；\

这个方法太粗暴。。。

直方图的缺陷有：

高维空间中，$bin$的数目以指数级增长；\

$bin$值得选取不容易。

直方图的相关计算：
（也不局限于直方图，这些计算方法是很通用的，后面也会用到。）\
我们现在有数据点$x$，其是从概率密度$p(x)$中取样的。\
$x$落在区域$R$的概率是： $P(x\in R)=\int_Rp(x)dx$ 如果$R$非常小，体积为$V$，则$p(x)$几乎是常数： $P(x\in R)=\int_Rp(x)dx\approx p(x)V$ 如果$R$很大，则： $P(x\in R) = \frac{K}{N}\rightarrow p(x)\approx \frac{K}{NV}$ 其中$N$是数据总数，$K$是落在区域$R$内的数据数。

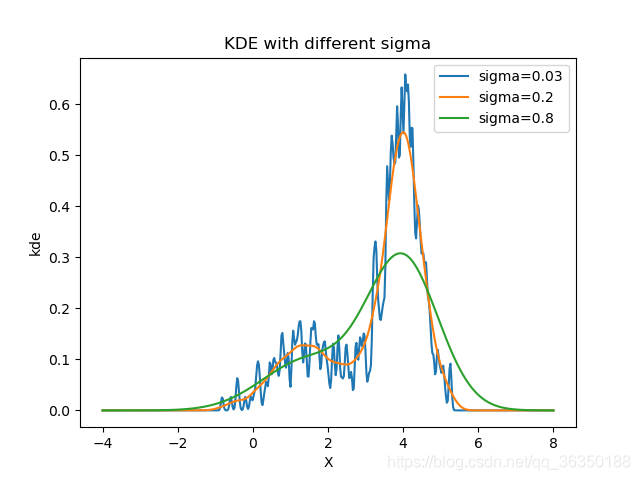
对于Kernel density estimation (KDE)，是固定$V$并确定$K$，比如说：确定固定在超立方体中的数据点$K$的数量，如下图示：

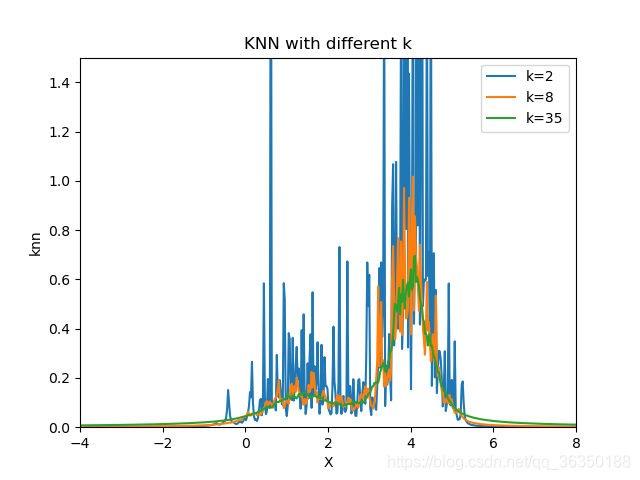
对于K-nearest neighbors (kNN)，是固定$K$并确定$V$，比如说：增加球的尺寸直到$K$个点都落在球内，如下图：

KDE

Parzen Window

对于一个$d$维，边长为$h$的超立方体，我们有如下关系：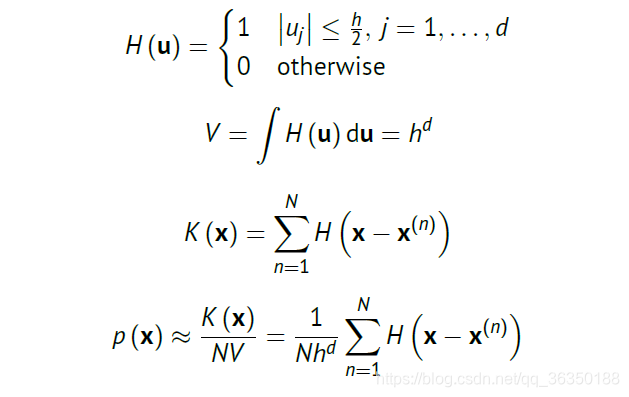

Gaussian Kernel

对于高斯核，我们则可以写成：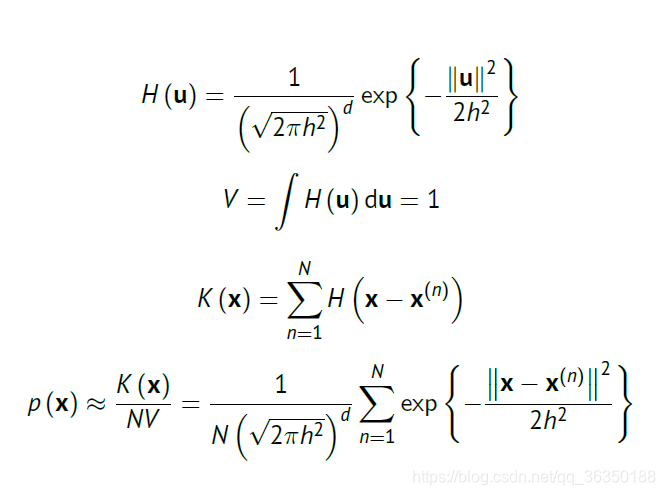

General Formulation – Arbitrary Kernel

对于更一般的形式，则有：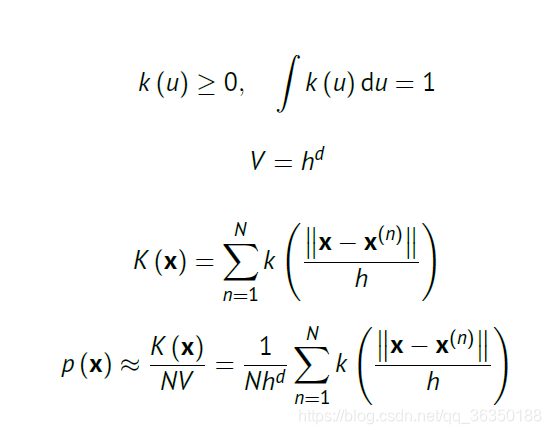

各种内核的总结

高斯核（Gaussian Kernel）

$k(u)=\frac{1}{\sqrt{2\pi}}exp\left\{-\frac{1}{2}u^2\right\}$

缺点是：

1. kernel has infinite support
2. Requires a lot of computation

Parzen window

缺点是：

1. Not very smooth results

Epanechnikov kernel

缺点是：

1. Smoother, but finite support

总结

核方法的缺点是：我们必须合适地选择核的带宽$h$。\
如果$h$太大则会过于平滑，太小则不够平滑。\
一个高斯核的例子：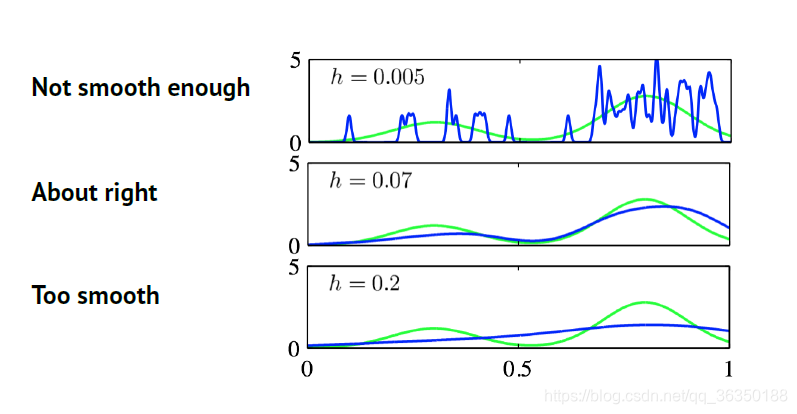

KNN

KNN分类大体意思是：假设我们的数据集有$N$个点，有$N_j$个点属于类$C_j$，并且有$\sum_jN_j=N$。现在要对点$x$进行分类，我们先画一个球，中心在$x$处，并且包含了（任意类的）$K$个点。假设球体积为$V$，且包含有$K_j$个点是属于$C_j$的，则我们有如下关系：

注意：与灰度图的$bins$和KDE的$h$类似，$K$值太大则会过于平滑，太小则不够平滑。

一个例子：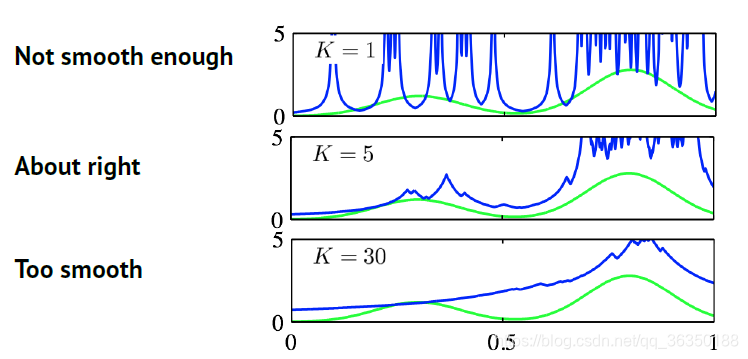

（附）作业相关代码

简单解释下作业：\
有两个数据集，分别为训练集和测试集，第1题要求画出不同$bins$下的直方图；第2题则是用高斯核，用不同的$\sigma$计算训练集的对数似然，比较差异性；第3题要求用不同的$K$值写$KNN$代码。\
代码如下：

import matplotlib.pyplot as plt
import numpy as np
from scipy.special import logsumexp

def load_data(path):
    data = np.loadtxt(path)
    return data

def plot_histogram(bins, arr):
    if len(bins) % 2 == 0:
        fir = len(bins) / 2 * 100
    else:
        fir = (len(bins) // 2 + 1) * 100
    
    pos = fir + 20 + 1
    interval = np.max(arr) - np.min(arr)
    for i in range(len(bins)):
        sub_bin = int(interval // bins[i]) + 1
        plt.subplot(pos+i)
        plt.hist(arr, bins = sub_bin, facecolor="blue", edgecolor="black", alpha=0.7)
        plt.title("Bin = %.3f" % bins[i])
        plt.xlabel('data')
        plt.ylabel('times')


def kernel_density_estimate(x_arr, x_lst, sigma):
    def _H_Gauss(h, u, d):
        H_u = np.exp(-(np.linalg.norm(u) ** 2) / (2 * h * h)) \
              / (np.sqrt(2 * np.pi * h * h) ** d)
        return H_u

    def _K(N, x, x_arr, h, d):
        k = 0
        for i in range(N):
            u = x - x_arr[i]
            k += _H_Gauss(h, u, d)
        return k

    def p(N, x, x_arr, h, d, V):
        p_x = _K(N, x, x_arr, h, d) / (N * V)
        return p_x
    
    V = 1
    N = len(x_arr.flatten())
    p_x_lst = []
    d = len(x_arr.flatten())/(x_arr.shape[0])
    for x in x_lst:
        temp_p = p(N, x, x_arr, sigma, d, V)
        p_x_lst.append(temp_p)
    return p_x_lst


def _logsumexp(x):
    return np.log(np.sum(np.exp(x)))

def ked_log_likelihood(x_arr, x_lst, sigma):
    N = x_arr.shape[0]
    ll_lst = []
    for x in x_lst:
        single_val = _logsumexp(-np.linalg.norm(x_arr.reshape(-1,1) - x, axis=1) ** 2 / (2 * sigma * sigma) \
                               - np.log(np.sqrt(2 * np.pi * sigma * sigma) * N))
        ll_lst.append(single_val)


    return np.sum(ll_lst)
        

def kNN(data, x_lst, k):
    knn_lst = []
    N = len(data.flatten())
    for x in x_lst:
        u = np.linalg.norm(x - data.reshape(-1,1), axis = 1)
        r = np.sort(u)[k-1]
        v = 2 * r
        temp_p = k / (N * v)
        knn_lst.append(temp_p)

    return knn_lst, np.sum(np.log(knn_lst))
    
    
def Comparison_NPM(data, test_data, k_lst, sigma_lst):
    for s in sigma_lst:
        temp_kde_test = ked_log_likelihood(data, test_data, s)
        temp_kde_train = ked_log_likelihood(data, data, s)
        print('train_data: log_likelihood of KDE with sigma = %.2f: %.12f' % (s, temp_kde_train) )
        print('test_data : log_likelihood of KDE with sigma = %.2f: %.12f' % (s, temp_kde_test) )

    for k in k_lst:
        _, temp_knn_test = kNN(data, test_data, k)
        _, temp_knn_train = kNN(data, data, k)
        print('train_data: log_likelihood of KDE with k = %d: %.12f' % (k, temp_knn_train) )
        print('test_data : log_likelihood of KDE with k = %d: %.12f' % (k, temp_knn_test) )        

def main():
    path = "./dataSets/nonParamTrain.txt"
    path_test = './dataSets/nonParamTest.txt'
    data = load_data(path)
    data_test = load_data(path_test)
    bins_w = [0.02, 0.5, 2.0]
    plot_histogram(bins_w, data)
    plt.tight_layout()
    plt.show()

    num = len(data.flatten())

    p_x = []
    p_test = []
    sigma = [0.03, 0.2, 0.8]
    x_lst = np.linspace(-4, 8, data.shape[0])
    for h in sigma:
        temp_p = kernel_density_estimate(data, x_lst, h)
        p_x.append(temp_p)
    for x in p_x:
        plt.plot(x_lst, x)
    plt.xlabel("X")
    plt.ylabel("kde")
    plt.legend(['sigma=0.03','sigma=0.2','sigma=0.8'])
    plt.title('KDE with different sigma')
    plt.show()


    k = [2, 8, 35]
    knn_lst = []
    for sub_k in k:
        temp_knn, _ = kNN(data, x_lst, sub_k)
        knn_lst.append(temp_knn)
    for knn in knn_lst:
        plt.plot(x_lst, knn)
    plt.xlabel("X")
    plt.ylabel("knn")
    plt.axis([-4, 8, 0, 1.5])
    plt.legend(['k=2','k=8','k=35'])
    plt.title('KNN with different k')
    plt.show()

    Comparison_NPM(data, data_test, k, sigma)


if __name__ == "__main__":
    main()

结果显示如下：

SuperZLW's Blog

概率密度估计（Probability Density Estimation）--Part 2：无参估计

引入

直方图（Histograms）

KDE

Parzen Window

Gaussian Kernel

General Formulation – Arbitrary Kernel

各种内核的总结

高斯核（Gaussian Kernel）

Parzen window

Epanechnikov kernel

总结

KNN

（附）作业相关代码