引入
在结束了有参估计,无参估计后,现在记录混合模型(Mixture models)。这里附一张有参和无参的对比图(本来应该附在Part 2的,不想回去改了。。):
字面意思,混合模型就是有参模型和无参模型的混合。
举个例子,高斯模型的混合(Mixture of Gaussians,MoG)。\
现有三个高斯模型如下:
我们可以将其视为:
其概率密度可以近似表示为:各变量有如下关系:
大概解释一下:$p(x|j)$表示第$j$个高斯模型的概率密度,$p(j)=\pi_j$表示第$j$个高斯模型出现的概率,是一种先验概率。\
这里记住两点:
即是说,混合模型概率密度积分为1,然后对于混合模型的每个子模型,我们都要求出对应的三个值(均值,方差和模型先验),这是对于MoG而言的。
求解方法
MLE法
对于简单的(单个)高斯模型,我们可以用MLE近似求解,但在高斯混合中无法使用该方法,因为我们在求参数时并不知道这个参数属于高斯混合的哪个子分布。如下:
这个$p(j|x)$我们是无法观测到的,毕竟如果这个都知道,那高斯混合就只是多个高斯模型的简单叠加而已。\
也就是说单个高斯模型的参数会取决于所有高斯模型的参数。所以MLE不可用。
Clustering
分为两种:
- Clustering with soft assignments\
- Clustering with hard assignments
简单说的话,hard assignments是根据Label划分的,也就是说每个数据点只属于一个label,比如说K-mean;soft assignment是根据概率区分的,每个数据点可能属于多个label,但概率不同。如下图:
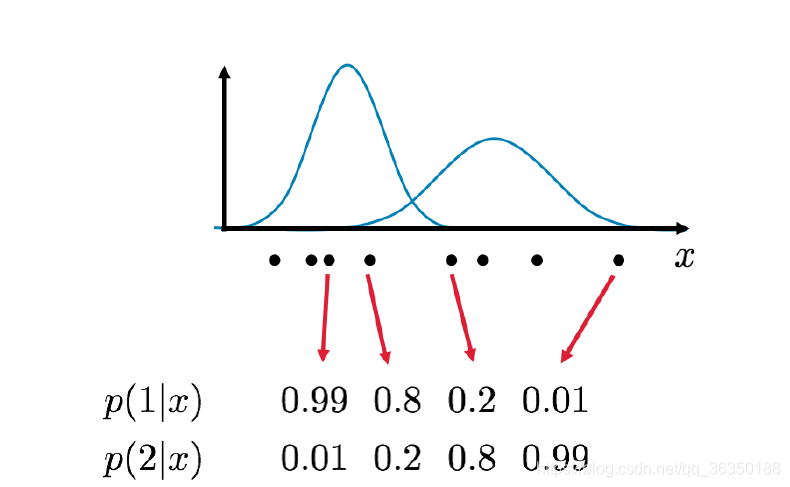
这里只介绍soft assignment,毕竟两个几乎是一样的。这就要用到这章的重点了,$EM$算法。
$EM$算法
大概的说明
$EM$算法是一种迭代算法,本质上它也是一种最大似然估计的方法,其特点是,当我们的数据不完整时,比如说只有观测数据,缺乏隐含数据时,可以用EM算法进行迭代推导。\
该算法包括$E$步骤和$M$步骤,这里不具体介绍一般性的$EM$算法,主要说明其在高斯混合中如何运用。其步骤大体可以概括为:
- 随机初始化各子分布的期望$\mu_1,\mu_2…\mu_m$。
- E-step:计算每个子分布的后验
- M-step计算所有数据点的加权平均值
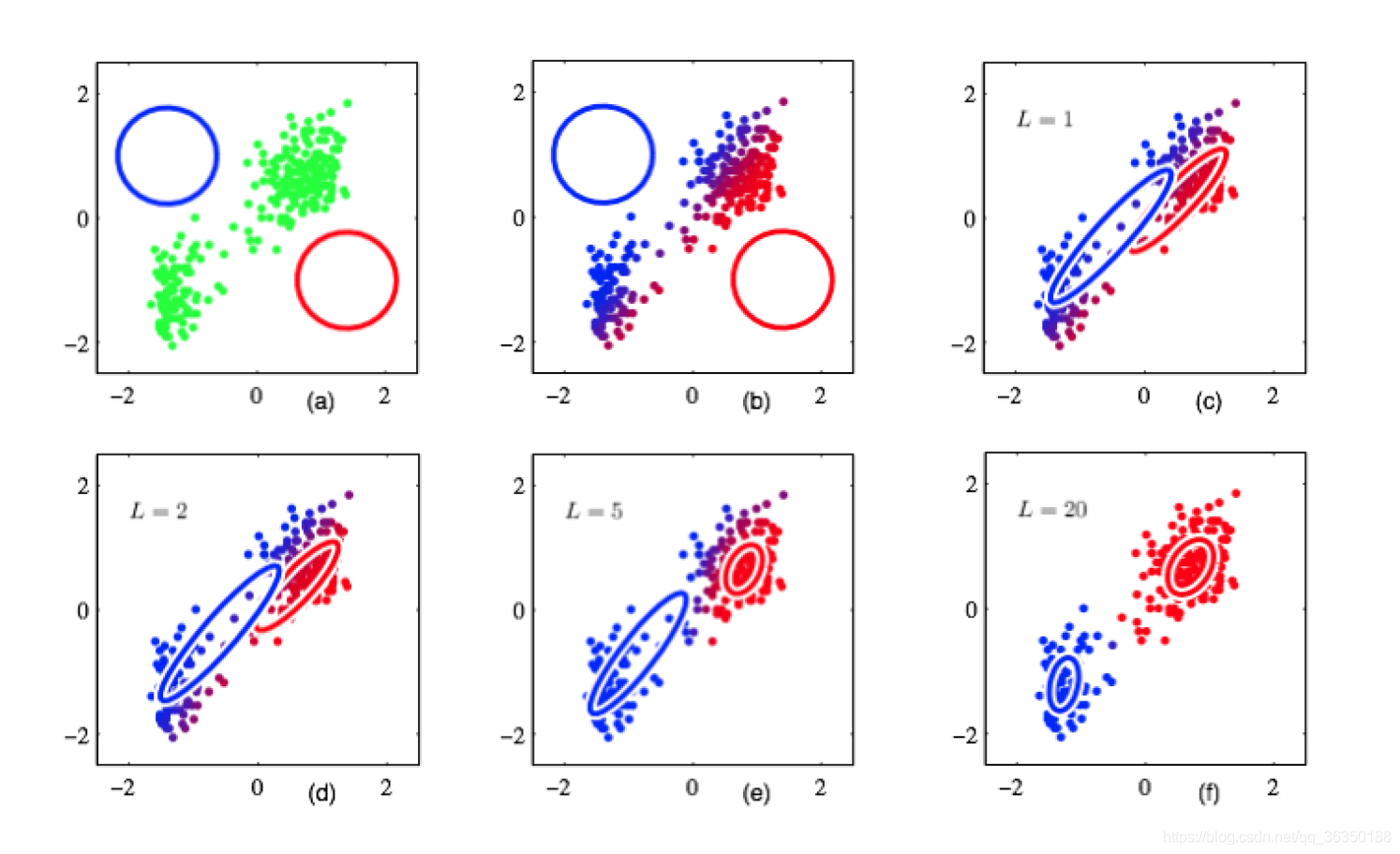
其效果如下图所示:
较为详细的说明
现在说一下更加详细的步骤。\
假设现在有两组数据,即是观测数据和隐藏数据:
- Incomplete (observed) data: $X={(X_1, X_2, … ,X_n)}$
- Hidden (unobserved) data: $Y=(Y_1, Y_2,…,Y_n)$
组合后形参完整数据:
- Complete data: $Z=(X,Y)$
联合密度为即是在高斯混合中:\
$p(X|\theta)$是混合模型的似然\
$p(Y|X,\theta)$是混合模型中子分布的估计
对于不完整的数据(观测数据),其似然为:对于完整数据(Z),其似然为: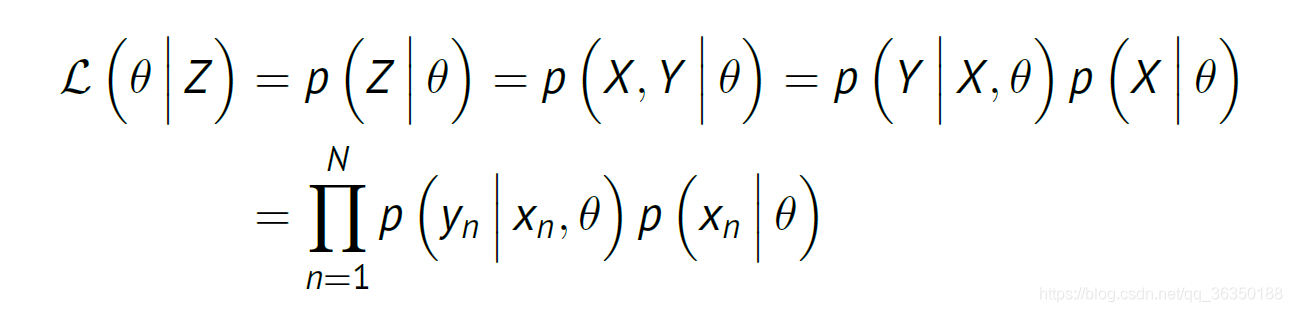
在这里我们虽然不知道$Y$,但如果我们知道当前的参数猜测$\theta^{i-1}$,我们就能用它来预测$Y$。\
在这里我们计算完整数据的对数似然的期望,如下: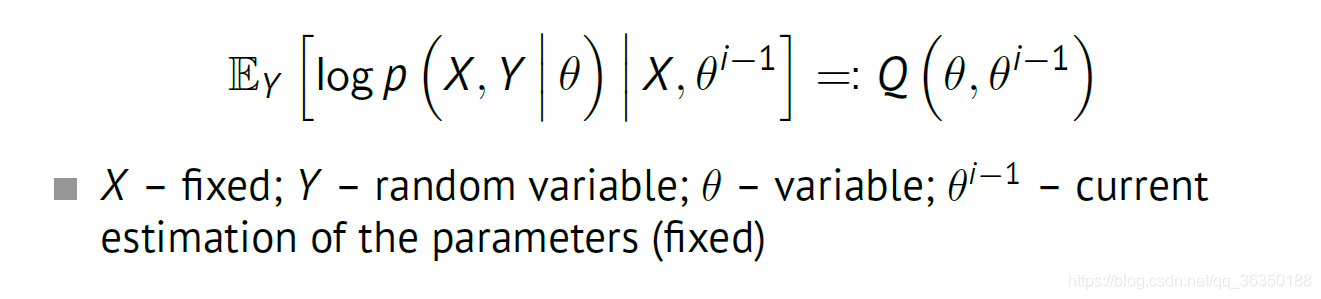
其中$X$和$\theta^{i-1}$是已知的。更进一步展开如下: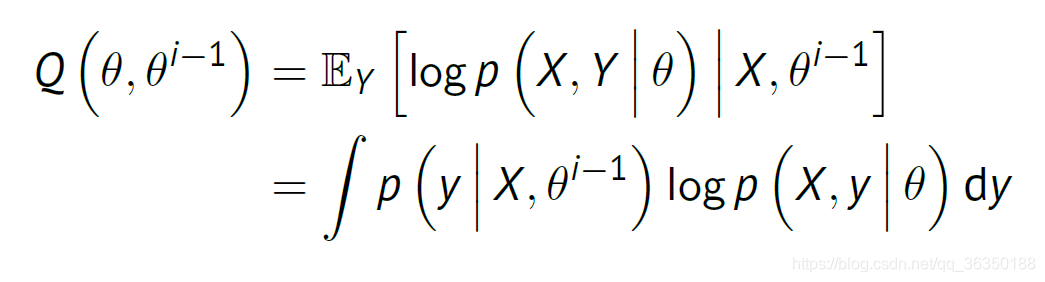
这个等式是根据均值和积分的关系写出来的。即是如下关系:\
这是一种迭代运算,我们要确保每次迭代中,第$i$次的结果至少和第$i-1$的一样好,即是:
若该期望值对于$\theta$来说是最大的,则可以认为(==这部分未理解==):
也就是说,在每次迭代中观测数据的对数似然都会不断增大(或者至少保持不变),最终达到局部最大值。\
所以,在实际运用中,初始化对于$EM$算法很重要,一个不好的初始化可能会使结果停在一个不好的局部最优值中。
高斯混合中的$EM$算法(EM for Gaussian Mixtures)
步骤:
- 初始化参数$\mu_1,\sigma_1, \pi_1…$\
循环,直到满足终止条件:
- E-step: 计算每个数据点对于每个子分布的后验分布:

这里的$\alpha$可以理解成每个数据点属于各个子分布的权重或者说概率。\ - M-step: 使用E步骤的权重进行更新数据:
 至此,高斯混合的$EM$算法就结束了,然后还有最后一个问题,这部分不太理解,但把结论贴上来吧,以后再探究:
至此,高斯混合的$EM$算法就结束了,然后还有最后一个问题,这部分不太理解,但把结论贴上来吧,以后再探究:
- E-step: 计算每个数据点对于每个子分布的后验分布:

(附)作业相关代码

也就是给出数据点,然后用EM算法进行高斯拟合:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
def load_data(path):
return np.loadtxt(path)
def init_params(k, d = 2):
pi = np.ones(k) * 1/k
mu = [np.random.rand(2, 1) for i in range(k)]
cov = [np.eye(2) for i in range(k)]
return pi, mu, cov
def EM(iter_times, data, k):
pi, mu, cov = init_params(k)
N = data.shape[0]
alpha = np.zeros((N, k))
likelihood_list = []
def update_alpha(alpha, N, k):
for i in range(N):
for j in range(k):
p_ij = pi[j] * multivariate_normal.pdf(data[i], mu[j].flatten(), cov[j])
alpha[i][j] = p_ij
likelihood[i] += p_ij
alpha[i] = alpha[i] / np.sum(alpha[i])
return alpha
sigma = np.empty((N, 2, 2))
for i in range(N):
d = data[i, :].reshape(2, -1)
sigma[i] = np.dot(d, d.T)
for i in range(iter_times):
likelihood = np.zeros(N)
# E-step: update alpha
alpha = update_alpha(alpha, N, k)
likelihood_list.append(np.sum(np.log(likelihood)))
# M-step: update mu, cov, pi
N_j = np.sum(alpha, axis = 0)
for j in range(k):
# update mu
alpha_x = 0
alpha_x_mu = 0
for n in range(N):
alpha_x += (alpha[n][j] * data[n])
alpha_x = alpha_x.reshape(2,1)
mu[j] = alpha_x / N_j[j]
# update pi
pi[j] = N_j[j] / N
# update cov
for n in range(N):
alpha_x_mu += alpha[n][j]*(data[n] - mu[j].T)*(data[n] - mu[j].T).T
cov[j] = alpha_x_mu / N_j[j]
plot_contour(iter_times, data, mu, cov, k)
if iter_times == 30:
plt.figure()
plt.plot(np.arange(1, 31), np.array(likelihood_list))
plt.title('log-likelihood for every iteration')
plt.xlabel('iteration')
plt.ylabel('log-likelihood')
plt.grid()
plt.show()
def plot_contour(iter_num, data, mu, cov, k):
plt.figure()
plt.title("iter_num = %d" % iter_num)
plt.scatter(data[:,0], data[:,1])
x_min, x_max = plt.gca().get_xlim()
y_min, y_max = plt.gca().get_ylim()
num = 50
x = np.linspace(x_min, x_max, num)
y = np.linspace(y_min, y_max, num)
X, Y = np.meshgrid(x, y)
for sub_k in range(k):
Z = np.zeros_like(X)
for i in range(len(x)):
for j in range(len(y)):
z = multivariate_normal.pdf(np.array([[x[i]], [y[j]]]).flatten(), mu[sub_k].flatten(), cov[sub_k])
Z[j, i] = z
plt.contour(X, Y, Z)
plt.show()
path = "./dataSets/gmm.txt"
def main():
k = 4
iter_lst = [1, 3, 5, 10, 30]
pi, mu, cov = init_params(k)
data = load_data(path)
for i in iter_lst:
EM(i, data, k)
if __name__ == '__main__':
main()
效果如下图所示:
迭代1次: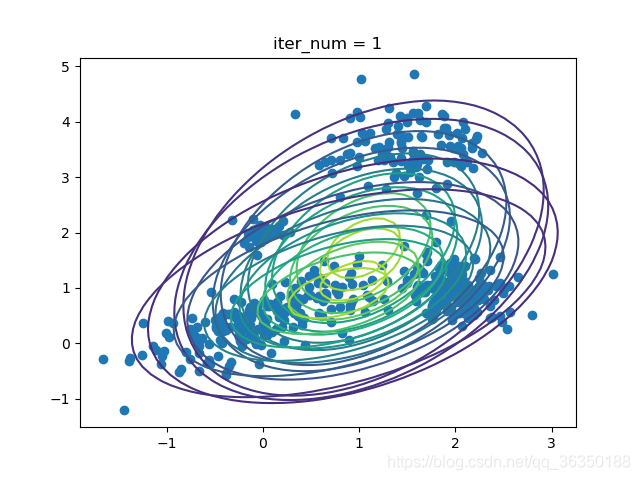
迭代3次: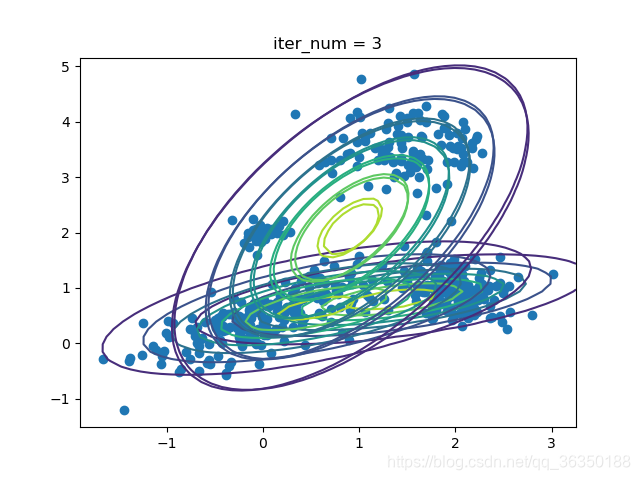
迭代5次: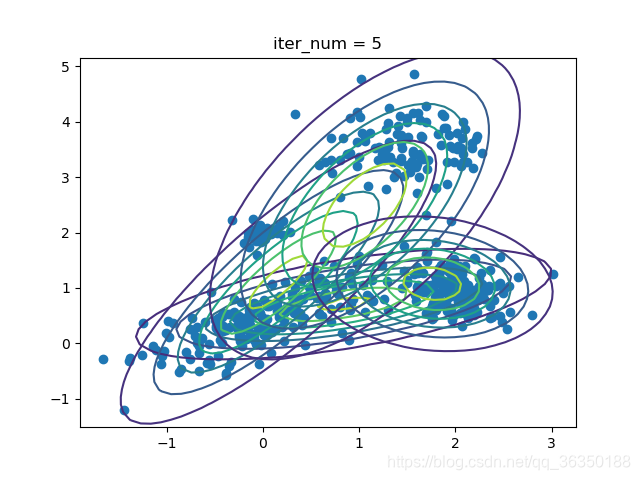
迭代10次:
迭代30次: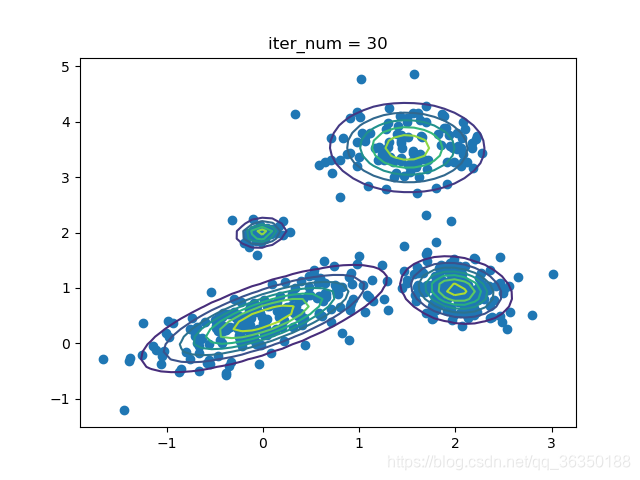
每次迭代的对数似然: