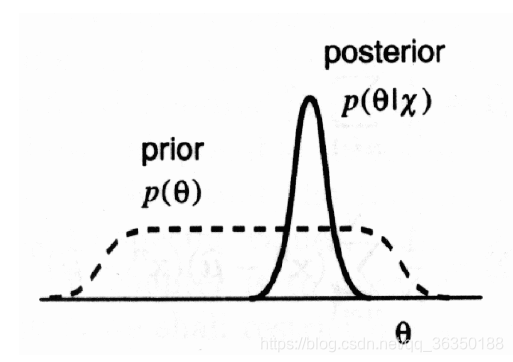
概率密度的引入

当我们有如下的点分布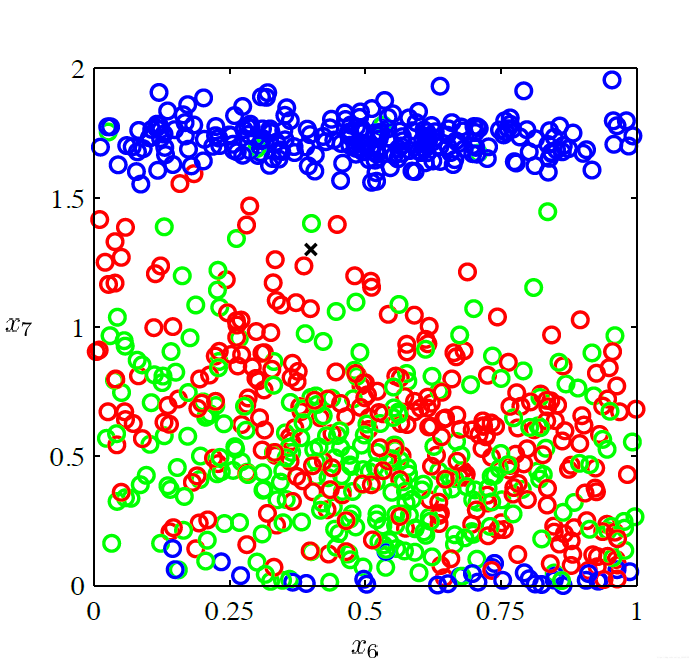

为了能区分它们，我们需要知道这些点的概率分布。常见的有贝叶斯最优分类(Bayes optimal classification)，这是基于如下的概率分布： $p(x|C_k)p(C_k)$
其中的先验$p(C_k)$很容易算，就是统计，或者说数数，现在的问题就成了计算如下的条件概率密度：$p(x|C_k)$。这主要有三种情况：

1. Parametric model
2. Non-parametric model
3. Mixture models

（简单解释一下，有参估计是指我们知道样本数据符合某种概率密度模型，通过给出的数据求出所需要的参数，比如高斯分布的均值和方差，有参估计的Robust比较好；无参估计是指我们不知道这些数据点符合哪些模型，所以无法求出其参数，这种情况在现实生活中更加常见）

参数模型（Parametric model）

概率密度模型的符号表示为： $x \sim p(x|\theta)$
以高斯模型为例： $p(x|\mu,\sigma)=\frac{1}{\sqrt{2\pi \sigma^2}}\exp \left\{ -\frac{(x-\mu)^2}{2\sigma^2}\right\}$
我们只要知道它的均值和方差就能完整地描述这个模型，即是： $\theta = (\mu, \sigma)$$$$x\sim p(x|\mu,\sigma)$ 现在我们需要根据模型和数据集求出$\theta$。\
其似然函数表示为：($X$为数据集数据)

$L(\theta)=p(X|\theta)$ 对于有参模型，这里介绍最大似然方法（Maximum Likelihood Method）

最大似然方法（Maximum Likelihood Method）

现假设我们有数据集$X=\left\{x_1,x_2,…,x_N\right\}$\
对于这些数据集我们假设数据是i.i.d(independent and identically
distributed)的，即是：

$P(x_1\le\alpha, x_2\le\beta)=P(x_1\le\alpha)P(x_2\le\beta)$\

$P(x_1\le\alpha)=P(x_2\le\alpha)$
通过该假设，似然计算可写为：

两边取对数为：

然后就是求导之类的事了。\
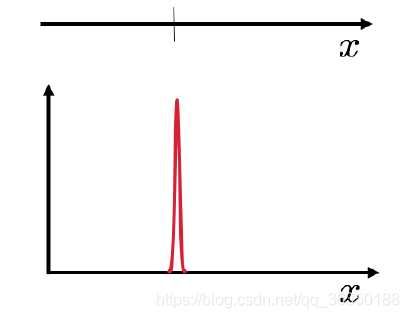
现在有个问题，如果$N=1$，即是说$X=\left\{x_1\right\}$，这时候产生的高斯模型会如下图所示：

看上去就像个$\delta$函数。\
这时候我们可以给平均数加上先验

贝叶斯估计（Bayesian Estimation）

与极大似然估计不同，贝叶斯估计假设待估计参数不是固定而是随机的。\
现在我们要根据给出的数据集$X$，得到$x$的密度函数$p(x)$。将其写成条件概率形式： $p(x|X)$ 用边缘概率和贝叶斯公式得出下图关系：

由于$p(x)$能根据$\theta$完全确定，即是说$\theta$是sufficient statistic，所以 $p(x|\theta, X) = p(x|\theta)$ 进而上面两个式子可写成：

（简单解释一下这个式子，$p(\theta |X)$表示估计参数对数据集$X$的依赖程度，也就是说$\theta$在一定程度上可以代指$X$，比如当$p(\theta|X)$在大多数地方都很小，但唯独在$\hat{\theta}$处很大，我们就能近似表示：$p(x|X) \approx p(x|\hat{\theta})$，该点也称为Bayes point）\
继续计算如下：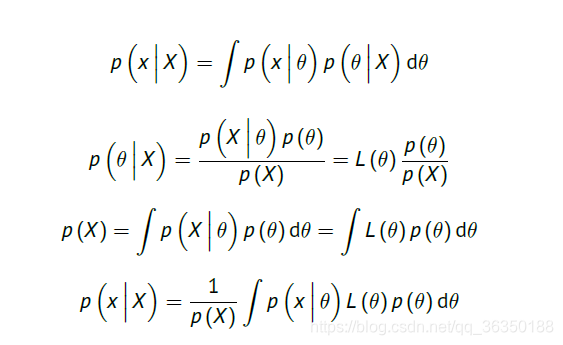

这里稍微对图里的参数进行解释：\
$p(\theta)$是估计参数的先验分布，它与给的数据集无关，而是我们的一种经验性判断。对于$p(\theta|X)$，是一个后验分布，所以一般取期望值，而且

举个例子：\
我们现在有高斯分布的数据集，其方差已知，我们要估计其均值，有如下关系：

对于先验我们的判断是：

根据采样均值和贝叶斯估计就能对均值进行估计：

最后这里补充个概念：

在贝叶斯统计中，如果后验分布与先验分布属于同类，则先验分布与后验分布被称为共轭分布，而先验分布被称为似然函数的共轭先验（Conjugate prior）。比如，高斯分布家族在高斯似然函数下与其自身共轭 (自共轭)。(来自 wiki百科)

比如上面那个均值的高斯先验，就是高斯模型的共轭，这里使用是因为：

The product of two Gaussians is a Gaussian.\

The marginal of a Gaussian is a Gaussian.

（附）参数估计的代码作业

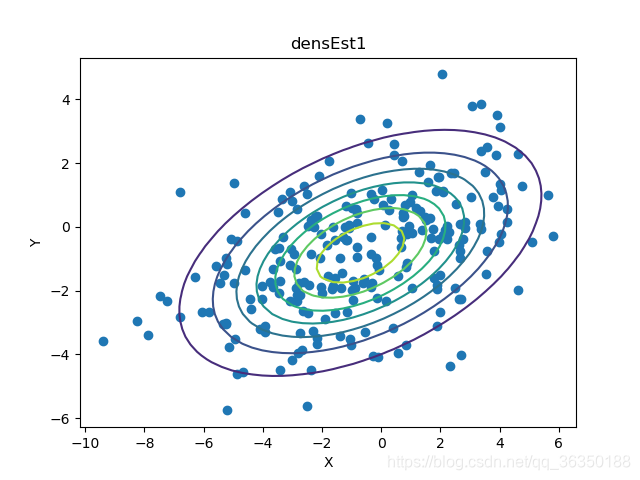
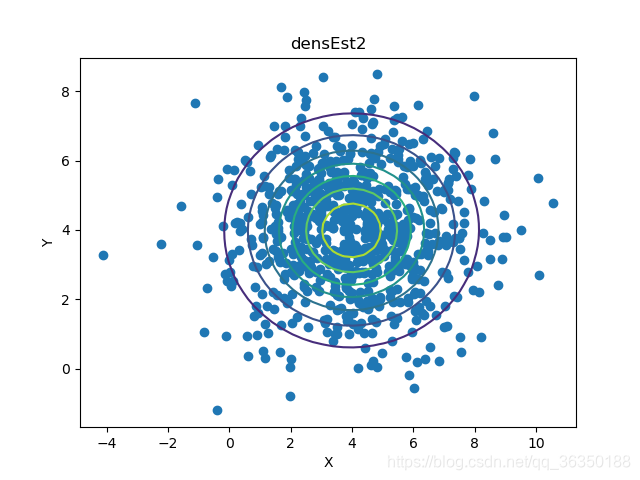
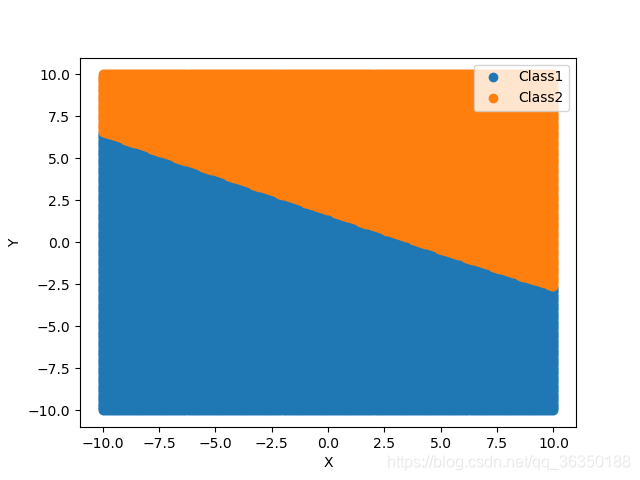
简单来说就是给两组二维数据，模型是高斯分布，进行参数估计拟合，第一题是纯粹的统计，跳过，第二题的话。。。还是直接附代码了吧（代码正确性未知，因为作业还没有公布结果）

def load_data(path):
    return np.loadtxt(path)

def prior_probability(arr_n, arr_sum):
    h_n, w_n = arr_n.shape
    h_sum, w_sum = arr_sum.shape
    p_n = (h_n * w_n) / (h_sum * w_sum)

    return p_n

def MLE_mean(arr):
    return np.mean(arr, axis = 0)

def bias_unbias_var(arr):
    num = arr.shape[0]
    arr_mean = MLE_mean(arr)
    dist = arr - arr_mean
    sum_vor_cov = np.zeros((2, 2))
    for i in range(num):
        ls = []
        ls.append(dist[i])
        dist_arr = np.array(ls)
        sum_vor_cov += np.dot(dist_arr.T, dist_arr)
        
    return sum_vor_cov / num, sum_vor_cov / (num - 1)
  

def two_dim_Gauss(x, mu, cov):
    #x = x.reshape(2, -1)
    p_x = np.exp((-0.5*(x - mu) @ np.linalg.inv(cov) @ (x - mu).T)) \
          / np.sqrt((2 * np.pi) ** 2 * np.linalg.det(cov))
    #print(p_x.shape)
    return p_x

def posterior(mu1, mu2, cov1, cov2, p_c1, p_c2):
    num = 300
    x = np.linspace(-10, 10, num)
    y = np.linspace(-10, 10, num)

    X,Y = np.meshgrid(x, y)
    C1 = []
    C2 = []
    for i in range(len(x)):
        for j in range(len(y)):
            z1 = two_dim_Gauss(np.array([[x[i], y[j]]]), mu1, cov1)
            z2 = two_dim_Gauss(np.array([[x[i], y[j]]]), mu2, cov2)
            temp1 = z1 * p_c1
            temp2 = z2 * p_c2
            if temp1 > temp2:
                C1.append(np.array([[x[i], y[j]]]))
            else:
                C2.append(np.array([[x[i], y[j]]]))
    C1 = np.array(C1).reshape(-1,2)
    C2 = np.array(C2).reshape(-1,2)

    plt.scatter(C1[:,0], C1[:,1])
    plt.scatter(C2[:,0], C2[:,1])
    plt.xlabel("X")
    plt.ylabel("Y")
    plt.legend(['Class1', 'Class2'])
    plt.show()
    


def plot_Gauss_point(arr, mu, cov):
    plt.figure()
    plt.scatter(arr[:,0], arr[:,1])
    x_min, x_max = plt.gca().get_xlim()
    y_min, y_max = plt.gca().get_ylim()


    num = 50
    x = np.linspace(x_min, x_max, num)
    y = np.linspace(y_min, y_max, num)
    X, Y = np.meshgrid(x, y)
    
    Z = np.zeros_like(X)
    for i in range(len(x)):
        for j in range(len(y)):
            z = two_dim_Gauss(np.array([[x[i], y[j]]]), mu, cov)
            Z[j][i] = z
    plt.contour(X,Y,Z)
    plt.xlabel('X')
    plt.ylabel('Y')
    
path1 = "./dataSets/densEst1.txt"
path2 = "./dataSets/densEst2.txt"

def main():
    arr1 = load_data(path1)
    arr2 = load_data(path2)

    arr_sum = np.vstack((arr1, arr2))

    p_C1 = prior_probability(arr1, arr_sum)
    p_C2 = prior_probability(arr2, arr_sum)

    mu2 = MLE_mean(arr2)
    bias_s2, sigma2 = bias_unbias_var(arr2)

    mu1 = MLE_mean(arr1)
    bias_s1, sigma1 = bias_unbias_var(arr1)

    print("The mean for C1 is: ", mu1)
    print("The mean for C2 is: ", mu2)
    print("The sigma with bias for C1 is", bias_s1)
    print("The sigma without bias for C1 is", sigma1)
    print("The sigma with bias for C2 is", bias_s2)
    print("The sigma without bias for C2 is", sigma2)
    
    plot_Gauss_point(arr1, mu1, sigma1)
    plt.title("densEst1")
    plot_Gauss_point(arr2, mu2, sigma2)
    plt.title("densEst2")
    plt.show()

    posterior(mu1, mu2, sigma1, sigma2, p_C1, p_C2)
    
if __name__ == "__main__":
    main()