Introduction
This blog is a summary of the papers I read recently, and it is also convenient for viewing at any time during the current project.
The project is based on viT semantic segmentation, so the papers here are related to it, including the following:
(Due to the limitations of English, the expression may be a bit strange, but as long as the meaning is correct, who cares?)
Attention is all you need
(The Chinese version can refer to my previous blog: here,
the content is different from this one, and relatively brief, but also could be very helpful to understand it.)
(Here I recommend a awesome blog.
Most of the pictures here are from this blog as well as my previous blog.)
WHAT? and WHY?
First, I will give a brief introduction to this paper from these two parts, and then elaborate on its principles later.
What is it?
“Attention” is a method proposed by Bengio’s team in 2014 and widely used in various deep learning fields.
On this basis, this paper further proposes a new concept: Transformer. As the title of the paper says,
the traditional CNN and RNN are abandoned in the Transformer,
and the entire network structure is completely composed of the Attention mechanism.
More precisely, the Transformer consists of and only consists of self-Attenion
and Feed Forward Neural Network.
A trainable neural network based on Transformer can be built by stacking Transformers.
The author’s experiment is to build an encoder-decoder with 6 layers
of encoder and decoder, and a total of 12 layers of Encoder-Decoder, which performed best
in machine translate.
Why use it?
The reason why the author uses “Attention” is to consider that the calculation
of RNN (or LSTM, GRU, etc.) is limited to sequential, that is to say,
RNN-related algorithms can only be calculated from left to right or from
right to left. The mechanism brings up two problems:
The calculation at time t depends on the calculation result at time t-1,
which limits the parallelism of the model;Information will be lost in the process of sequential calculation. Although
LSTM and other structures alleviate the problem of long-term dependence to a
certain extent, it is still powerless for particularly long-term dependence.
The proposal of Transformer solves the above two problems. First, it uses “Attention”
to reduce the distance between any two positions in the sequence to a constant; second,
it is not a sequential structure similar to RNN, so it has better Parallelism, in line
with existing GPU frameworks.
Said in the paper:
Transformer is the first transduction model relying entirely on self-attention to compute representations of its input and output without using sequence aligned RNNs or convolution。
Principle
Structure of the Transformer
Here take the machine translation as example, if we want to translate a sentence as below:
Expand the transformer module, we can see: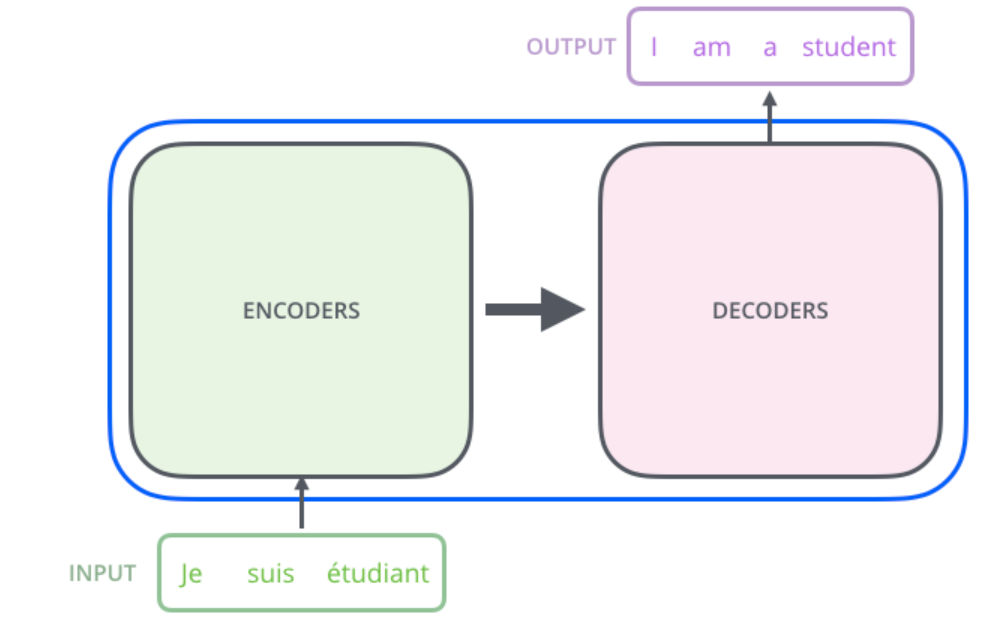
The Encoder-Decoder are what we mention above.
Further expand the module, we can get that: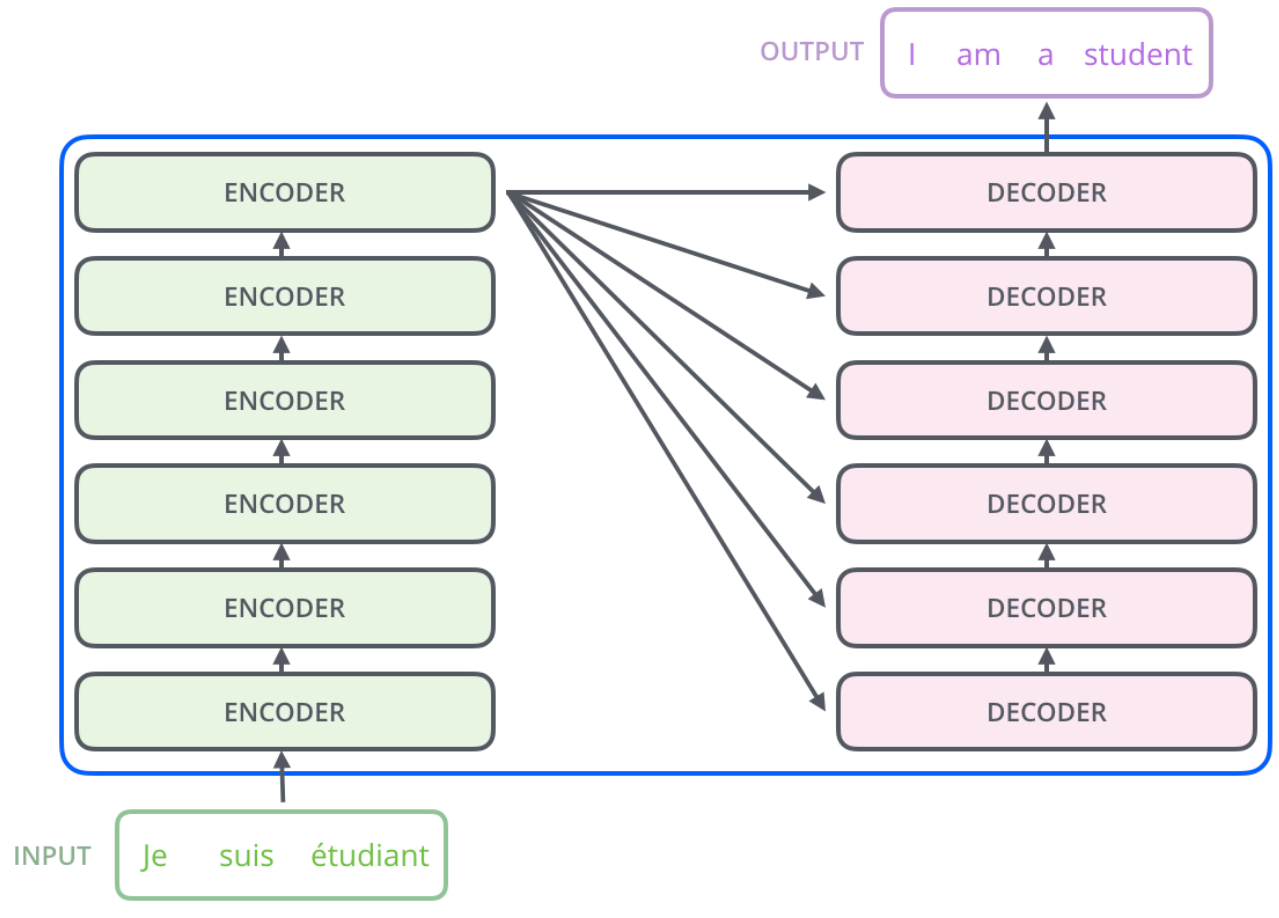
And the Encoder-Decoder looks like: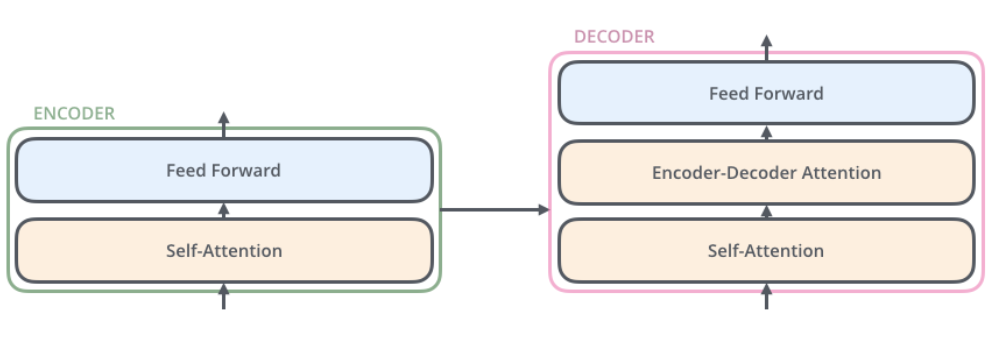
How it works
First of all, we need to do word-embedding as the input of
the first Encoder, all the encoder receive a list of vectors each
of the size 512, it means that, both word-embedding and
the output of a Encoder should be in the same size, that is,
list of vectors each of the size 512. This size(512) is
depended on the longest word of our training data, it should be
a hyperparameter.
We could see this figure, the FC layer is also named feed
forward layer.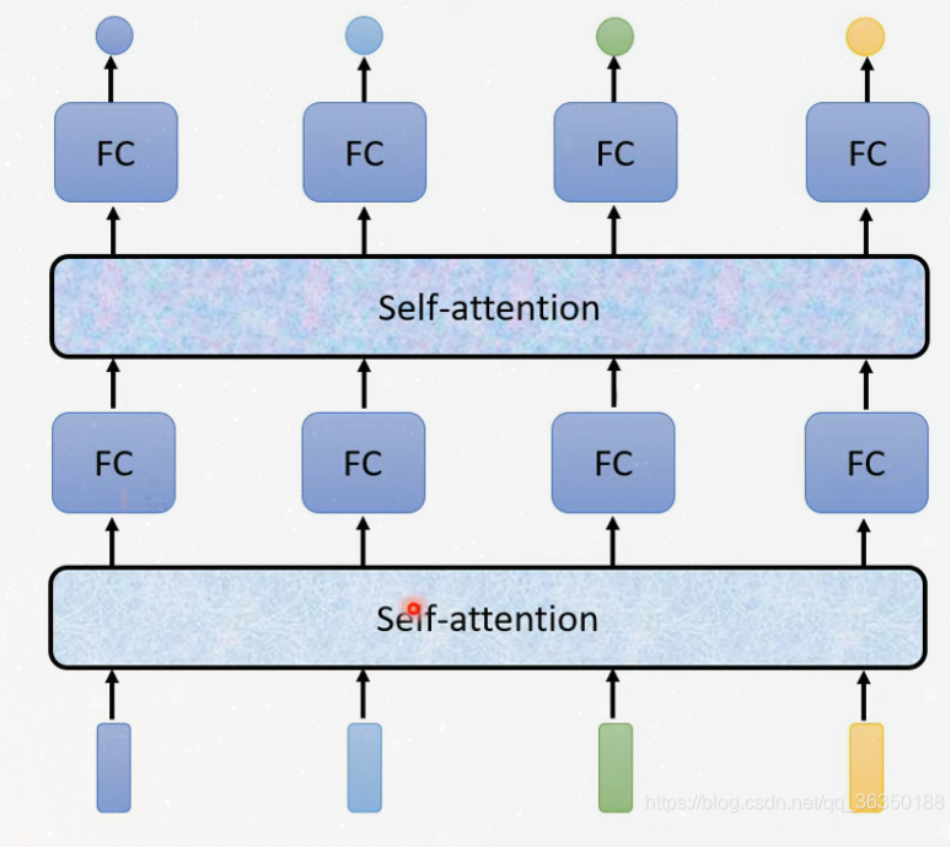
It shows that, after self-attention, there are dependencies
between these paths, but no dependencies in feed forward layer,
thus the various paths can be executed in parallel while
flowing through the feed-forward layer.
Detail of the “Self-Attention”
Step 1: create 3 vectors
After Embedding of one word, we get an embedding vector, with 512
size. Next, we need to create 3 new vector, named: Queries
Vector, Keys Vector and Values Vector. The size of these 3 vectors
should be smaller than Embedding Vector, usually, they could be 64.
But how can we obtain these 3 vectors?
Here we need 3 matrix, that is $W^q$, $W^k$ and $W^v$. We multiply embedding
vector by the $W^q$ to obtain vector q, that is, Queries Vector, and the same to get
other two vectors.
Step 2: compute scores
These scores are used to measure how much focus to place on other parts of the
input sentence as we encode a word at a certain position. For example, we have the
following sentence:
The animal didn’t cross the street because it was too tired
What does it mean here? Fur us, it is a quite easy question, but
computer does not think so. So it is necessary to compute this score.
Just like the figure below:
To calculate these scores, there are 2 common methods: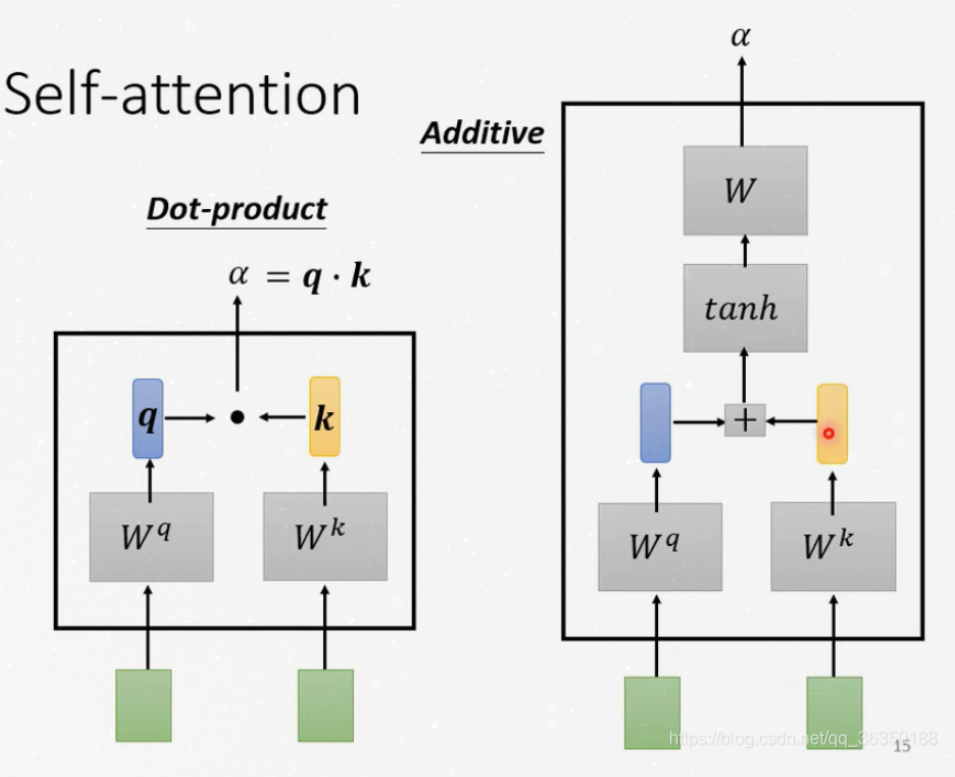
Here we only consider the left one. It means that, we use dot product
of the query vector with the key vector of the respective word we’re scoring.
Step 3, 4
Divide the score by 8 (the square root of the dimension of the key vectors
used in the paper), and then use SOftmax to normalizes the score.
Such as the figure below: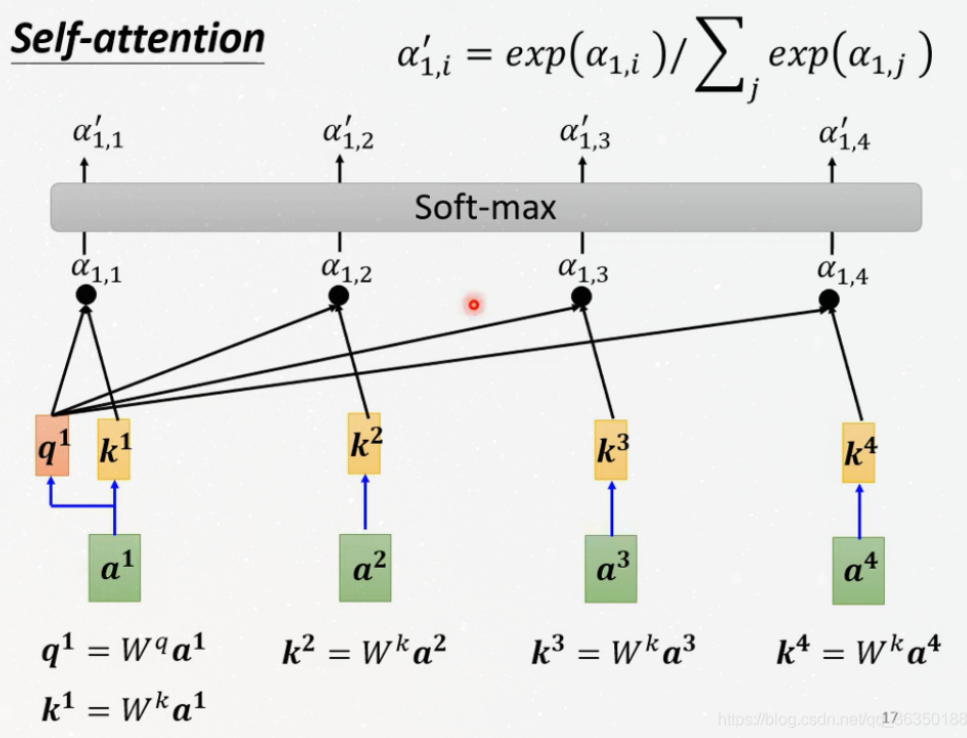
Note: the score of itself is also required and the
score above should first divide by 8, and then softmax. The activate
function could also be replaced by other function likes ReLU.
Step 5, 6
Multiply each value vector by the softmax score, this step
can be used to ignore the unrelated word.
And then sum up the weighted value vectors, to produces the
output of the self-attention layer at this position.
Such as the figure below: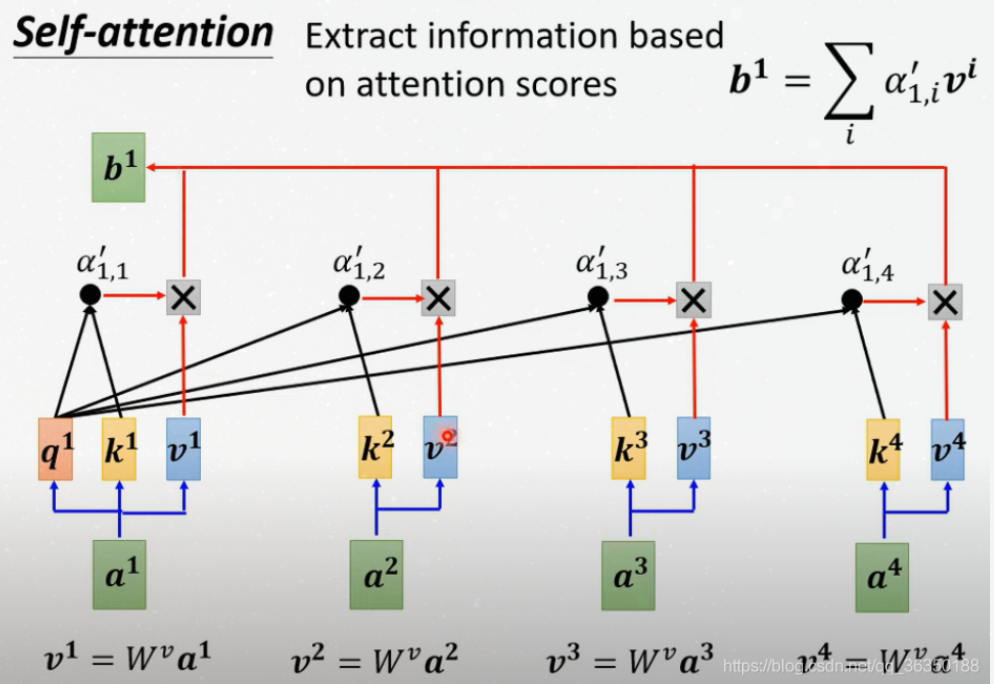
In Matrix Form
This part shows how to compute with matrix, several picture are
enough: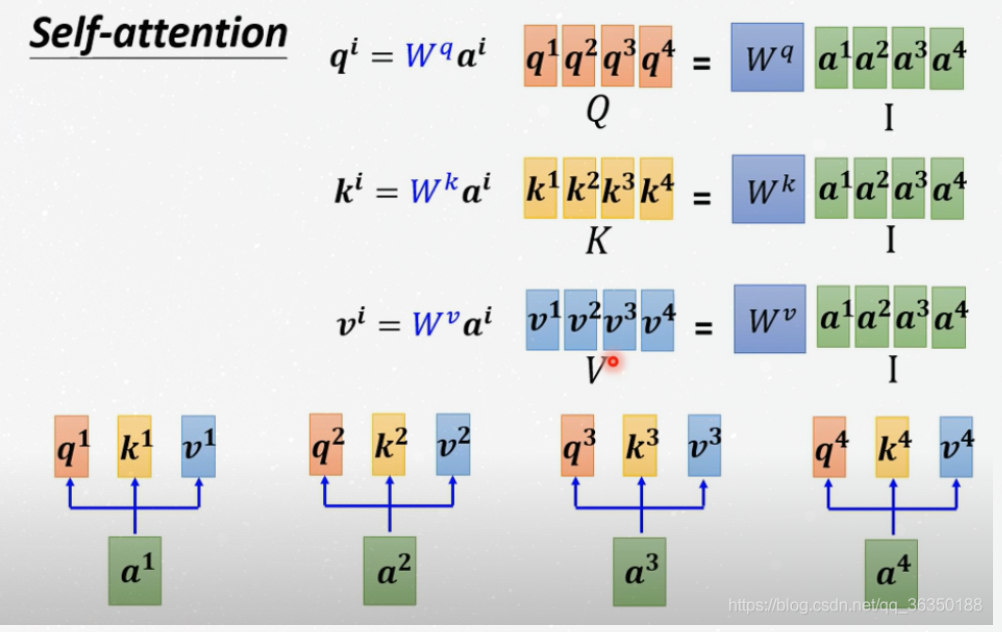
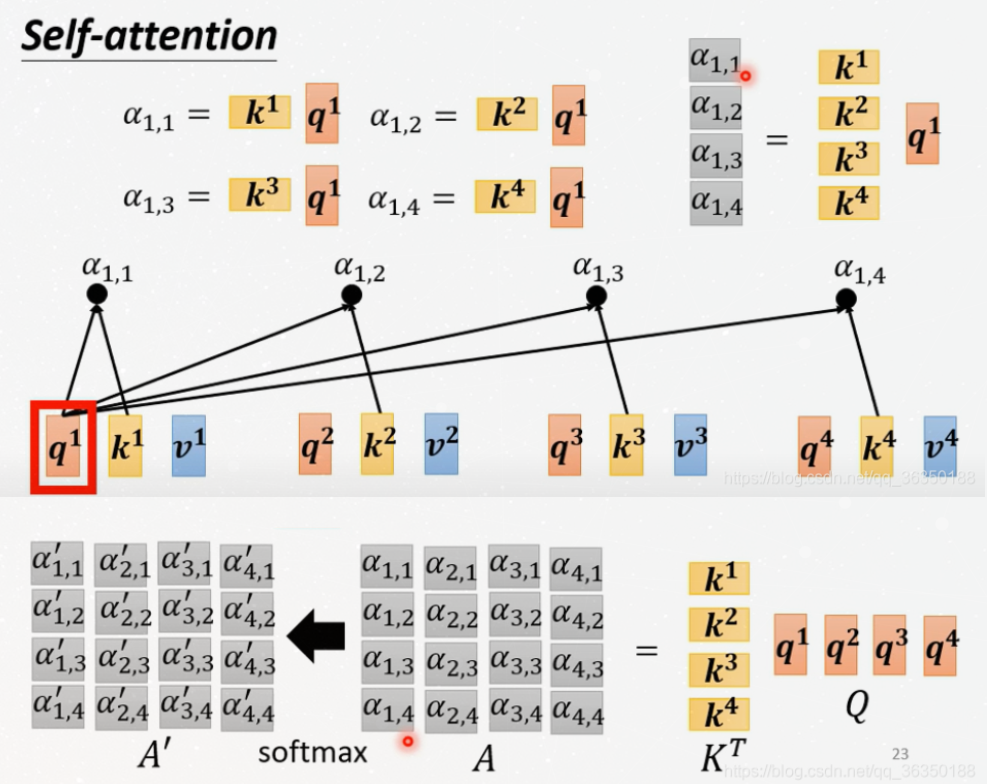
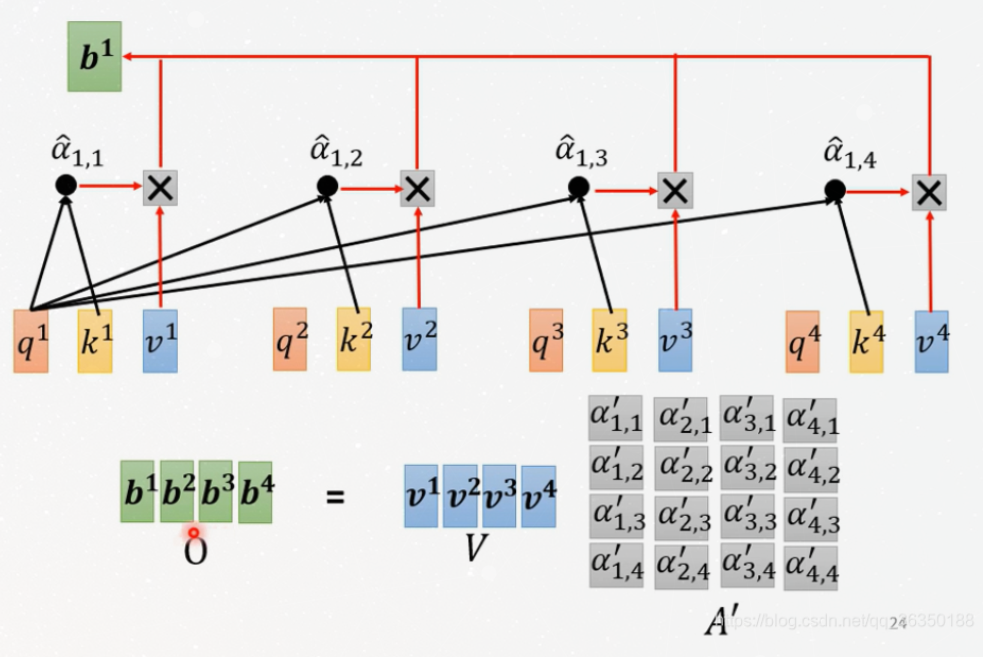
Note: Only $W^q$, $W^k$ and $W^v$ should be learned.
Multi-head-Self-attention
Use multi-head can improve the ability of the model to focus
on different positions. Take 2 heads as example: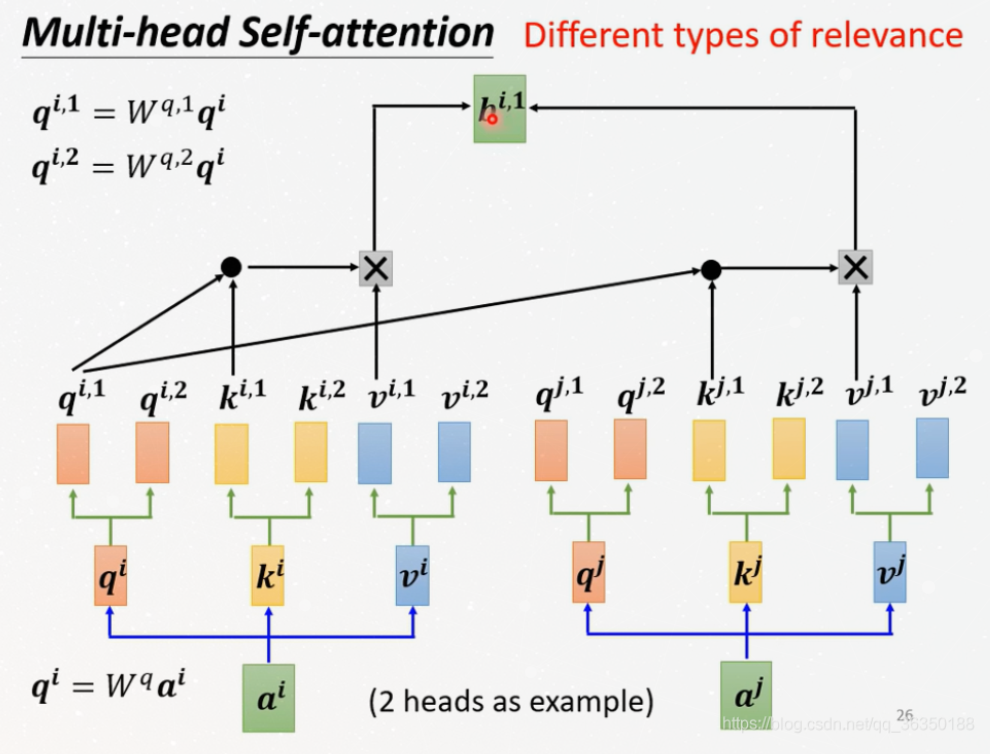
There are 2 sets of Query/Key/Value weight matrices, that means that,
we will get 2 $b$ by using one embedding vector, but we only need
one vector as input for next layer.
So here we introduce a new weight matrix $W^0$: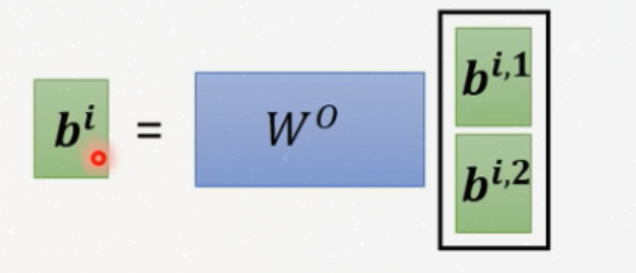
It means that, We concat the matrices then multiply them by an additional
weights matrix $W^0$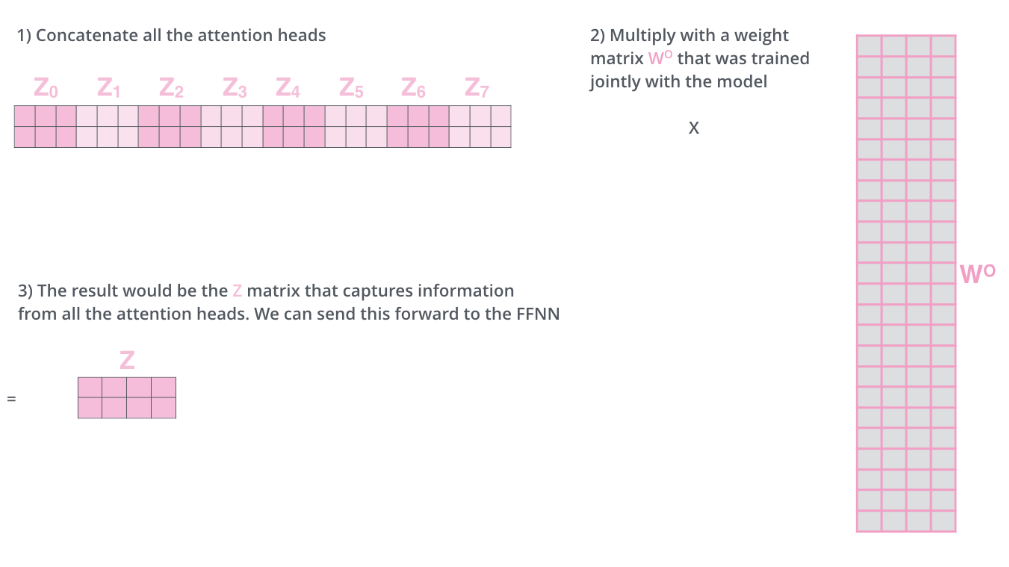
(this image takes 8 heads as example)
Position Encoding
The last problem is, although we consider the whole sentence, we do not consider
the relative position of the individual words.
To solve this problem, we need to use an additional vector, which
can tell the model the exactly position of each word, or the distance
between different word. And this vector could be considered in
embedding vector.
For example, if the dimension of the embedding vector is 4, it could
be: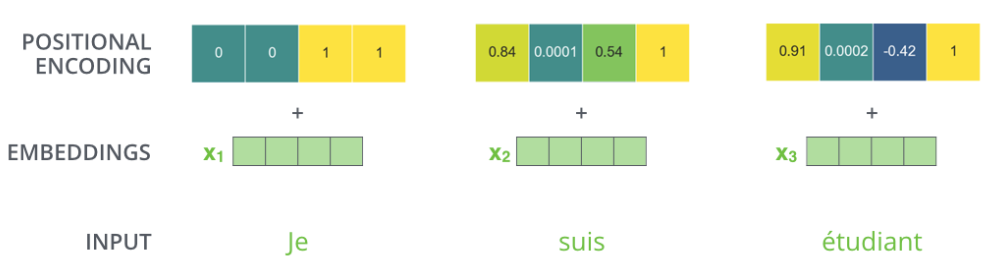
This position vector in paper looks like this: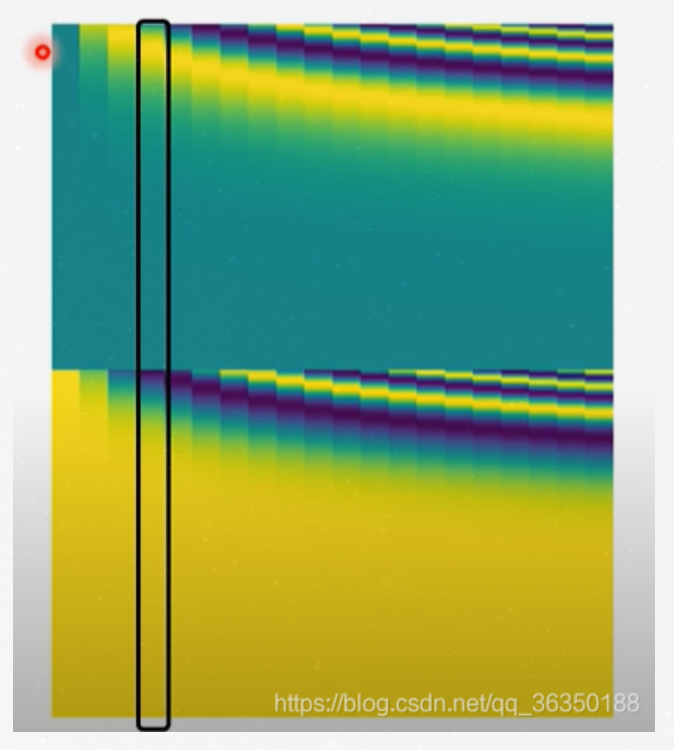
Each column represents a position vector. The first column will be
the vector we want to add to the first word embedding in the
input sequence. Each column contains 512 values, each with a value
between 1 and -1
A small detail
One detail in the encoder architecture is that each sub-layer
(self-attention, ffnn) in each encoder has a residual connection around it,
followed by a layer normalization step. Such like this: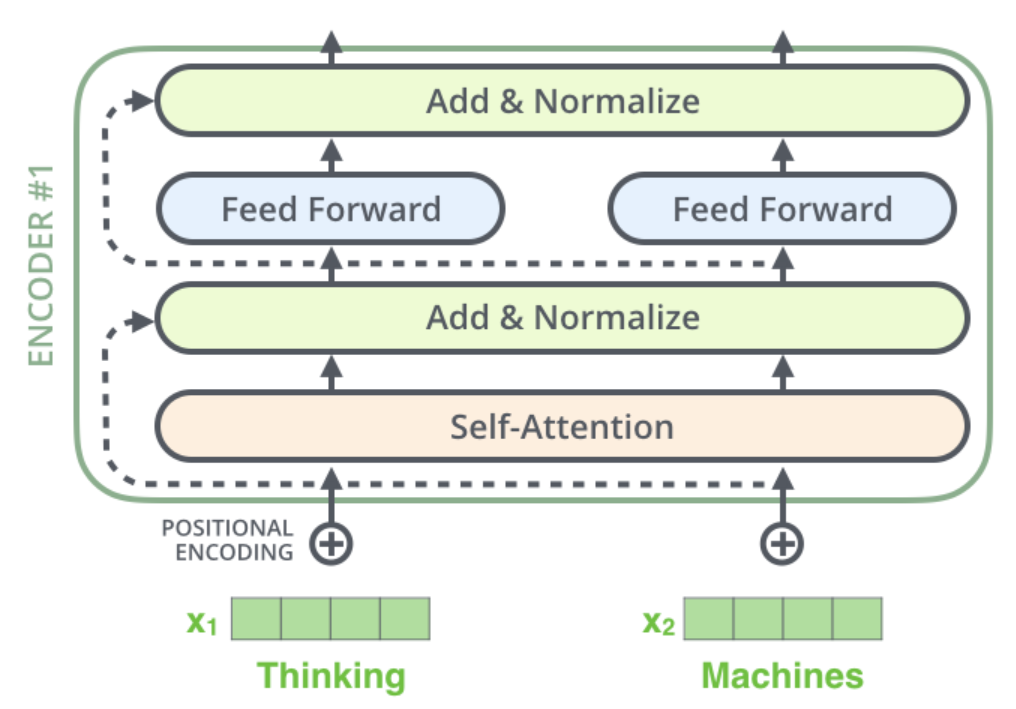
More specifically: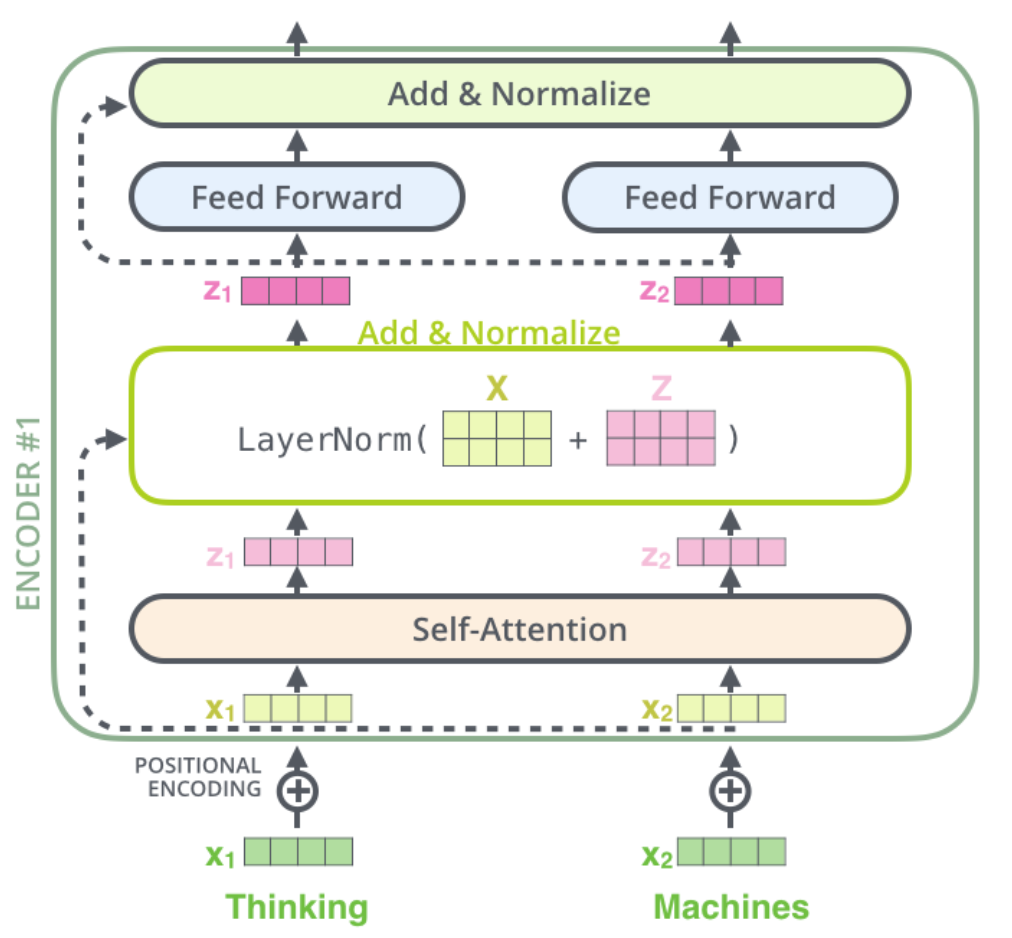
Decoder
After learning the principle of the Transformer as well as
the Encoder, now we could start our Decoder.
After processing the input sequence by encoder, the output of
the top encoder is then transformed into a set of attention vectors
K and V. These are to be used by each decoder in its “encoder-decoder
attention” layer which helps the decoder focus on appropriate places in
the input sequence: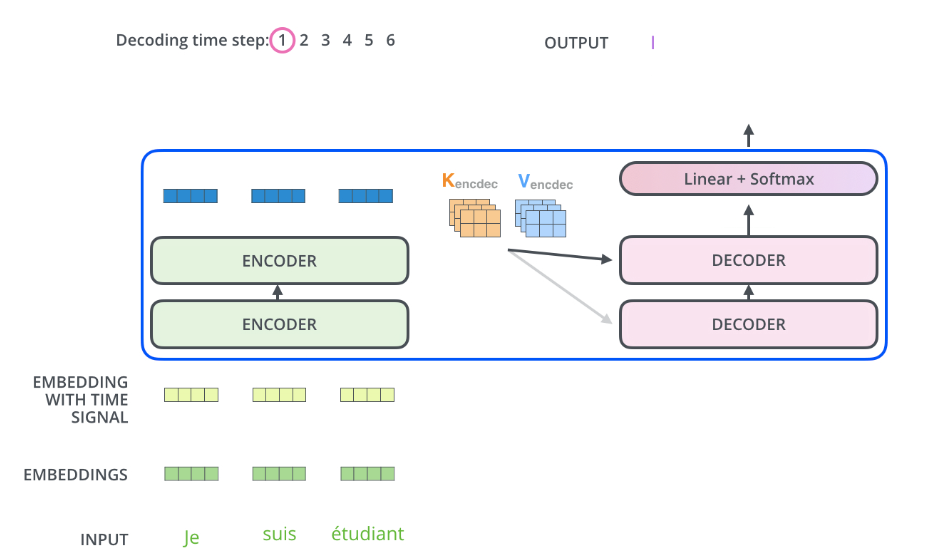
Repeat this process, until a special signal is outputted, to tell
the decoder that the process should be finished.
What’s more, the self-attention in decoder is a bit different from the
self-attention in encoder. In the decoder, the self-attention layer is only
allowed to attend to earlier positions in the output sequence.
This process can be showed as below: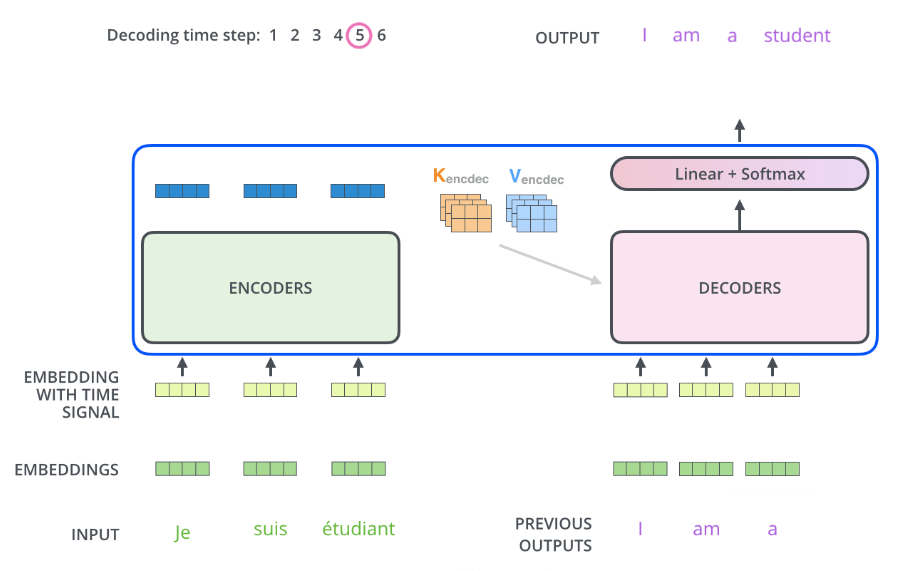
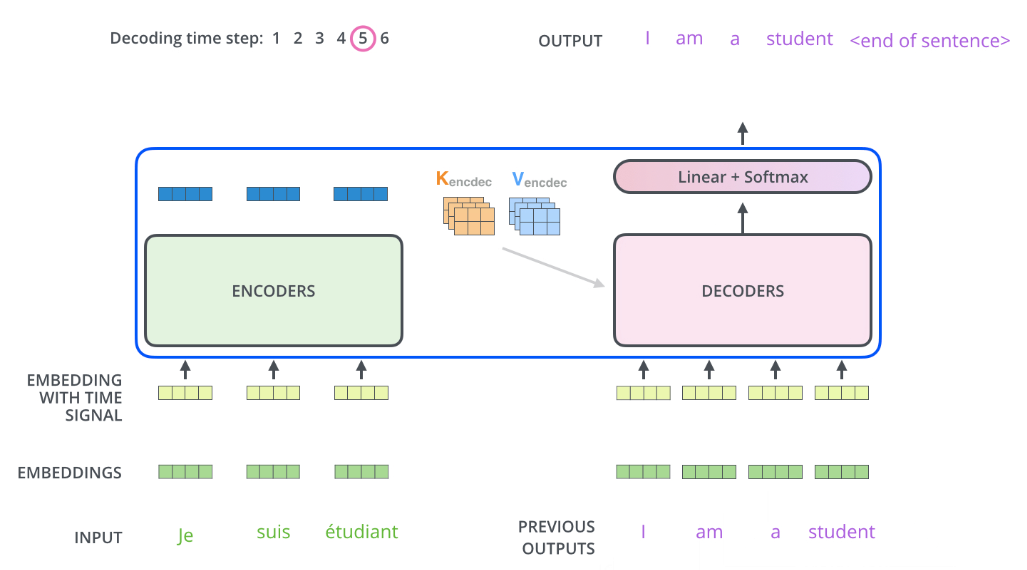
we could see that, the self-attention of decoder only care about
the earlier positions in the output sequence, for example, we use
“I”, “am”, “a” that we obtained before to get the new word “student”.
It should be noted that, the K and V vectors from encoder should be used
in every decoder part.
Finally, we get a float vector, we should turn it into a word, this is what
the last layer, softmax layer, do. It is a simple full connected layer,
that projects the vector produced by the stack of decoders, into a much,
much larger vector called a logits vector.
Reference
[1] Paper: Attention is all you need