SuperZLW's Blog

我很笨，但是我不懒

0%

方差分析

发表于 分类于 Valine：

引入

对于比较两个总体的均值，t-test 是个不错的选择，但假如我们现在有很多个总体呢，t-test 好像就变得不那么理想了，毕竟比较所有成分效率太低。\
我们需要一种检测方法，它可以告诉我们在这些总体的任意一个地方是否有任何显著的差异，如果没有的话，那我们就没必要进一步探究了。\
要分析均值间的方差，可以用 F test，或者又叫方差分析（Way Analysis of Variance，ANOVA）。

单因素方差分析

在试验过程中，只有一个因素在改变，称为单因素试验，而单因素方差分析主要用来验证这种试验中两组或两组以上的样本均值是否有显著性差异。\
举个例子，工厂有5台机器生产同一种零件，我们想知道这几台机器生产的零件重量（或者其它指标）是否一致，就可以转化为验证这5个总体的均值是否一致，这里考察的就是机器这一因素对零件重量有无影响。\
如下图（这个图跟这个例子不对应，但意思是一样的，即组内方差和组间方差，因为现在还不懂在这里要怎么画图。。）：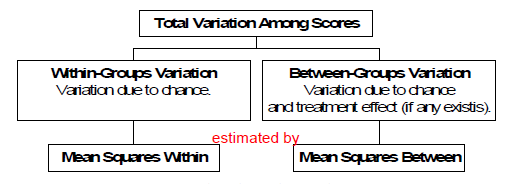
也就是说，F可以写为：

当：

  1. $F=1$: $H_0$ 为真，每组平均值之间有相同的变化量，与机器无关；
  2. $F>1$: $H_0$ 为假，平均值之间的巨大差异可能不是偶然造成的，表明至少存在一个机器与其它机器不同。

上面只是一个简单的例子，具体地，我们要根据样本的关系进行如下分类。

样本大小相等

现假设我们有 $m$ 组独立样本，每组样本有 $n$ 个元素，即可以写成：

我们做出如下假设：

$H_0$: $\mu_1=\mu_2=…=\mu_m$ vs $H_1$: 并非所有均值都相等。\

继续往下，方差分析这里最重要的就是计算组内以及组间方差，为此需要计算如下两种均值：

  1. 组内均值：令 $\overline{x}_{i\cdot}$ 为第 $i$ 组样本的均值，即：
  2. 总体均值：用$\overline{x}_{\cdot \cdot}$表示对$\mu$的估计，即：

然后通过下面表格就可以计算出F的值：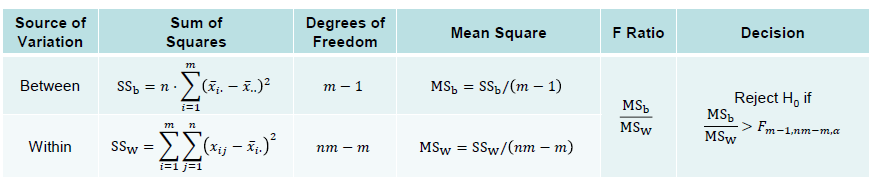

样本大小不等

现假设我们有 $m$ 组独立样本，每组样本有 $n_1,…,n_m$ 个元素，即可以写成：

同样我们做出如下假设：

$H_0$: $\mu_1=\mu_2=…=\mu_m$ vs $H_1$: 并非所有均值都相等。\

依旧计算两种均值：

  1. 组内均值：$\overline{x}_{i\cdot}=\sum_{j=1}^{n_i}\frac{x_{ij}}{n_i}$\
    \
  2. 总体均值：$\overline{x}_{\cdot \cdot} = \frac{\sum_{i=1}^m\sum_{j=1}^{n_i}x_{ij}}{\sum_{i=1}^mn_i}$

令 $N = \sum_in_i-m$。\
然后通过下面表格就可以计算出F的值：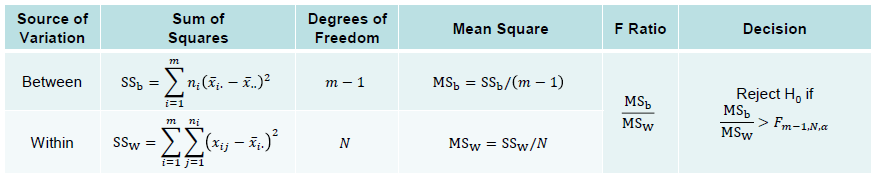

一个例子

下图表示从5种不同的方法中采集的数据，现在我们要判断这5种不同的方法是否会给出不同的结果。\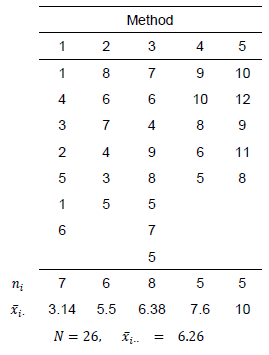

均值之类的都已经算好了，直接带入上面表格里的式子可得：

则均方根(mean Squares) 为：

测试统计量为：$\frac{MS_b}{MS_w}=11.19$\
通过查找F分布表可得：$F_{4,26,0.05}=2.743$\
由于11.19 > 2.743，所以拒绝零假设。

双因素方差分析

字面意思，这里的方差分析涉及到两个因素，比如说，我们要探讨不同温度及营养元素对培养皿微生物繁殖的影响，就可以使用双因素方差分析。\
另一个例子，如下图：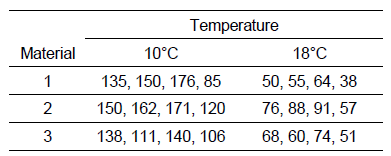
给出的是不同温度与材料下发动机的寿命(月)。\
计算跟单方差分析还是挺类似的，定义以下变量：$\mu,\alpha_i,\beta_j,\gamma_{ij},i=1,…,m,j=1,…,n$，并有如下关系：

  1. $\mu=\mu_{\cdot\cdot}$：总体平均值（即所有元素）;\
  2. $\alpha_i=\mu_{i\cdot}-\mu_{\cdot\cdot}$：第$i$行的影响;\
  3. $\beta_j=\mu_{\cdot j}-\mu_{\cdot\cdot}$：第$j$列的影响;\
  4. $\gamma_{ij}=\mu_{ij}-(\mu+\alpha_i+\beta_j)=\mu_{ij}-\mu_{i\cdot}-\mu_{\cdot j}+\mu_{\cdot\cdot}$：行𝑖和列𝑗的相互作用。\
    （这里 $\mu_{ij}=E[X_{ij}]$）

零假设这里有三个：

  1. $H_0^r: \alpha_i=0$, for all i（即是行没有影响）;\
  2. $H_0^c: \beta_j=0$, for all j（即是列没有影响）;\
  3. $H_0^{int}: \gamma_{ij}=0$, for all i, j（即是行列没有相互作用）。

更一般的情况，也就是每行每列多个观测值。\
现假设每行每列有 $l$ 个观测值，比如上面那张图里 $l=3$，并假设所有观测值都是独立的正态随机变量，方差均为 $\sigma^2$。\
假设数据表示为 $X_{ijk}$, $i=1,…,m \quad j=1,…,n \quad k=1,…,l$，则无偏估计为：

$\hat{\mu}=\overline{x}_{\cdot\cdot\cdot}$\
$\hat{\alpha}_i=\overline{x}_{i\cdot\cdot}-\overline{x}_{\cdot\cdot\cdot}$\
$\hat{\beta}_j=\overline{x}_{\cdot j \cdot}-\overline{x}_{\cdot \cdot\cdot}$\
$\hat{\gamma}_{ij}=\overline{x}_{ij\cdot}-\overline{x}_{\cdot j \cdot}+\overline{x}_{\cdot\cdot\cdot}$

最后就可以根据下图，计算，查表然后判断了：
可以拿上面那个发动机的数据计算，这里就不写了，就只是代公式而已，最后结果会是：拒绝$H_0^c$, 接受另外两个零假设。\

------ 本文结束------