假设性检测 (t-test, z-test)

引入

在实际生活中，我们处理的往往是很大量的数据，分析时经常要对这些数据的某种规律提出一个假设，但我们有时没法直接用总数据来验证这个假设，而是通过样本数据来推断，决定是否拒绝这一假设，这样的统计活动成为假设检验。\
假设检测方法的均值对比方法主要有t-test和z-test，以下介绍这两个检测以及中间涉及到的F-test。

该检测一般可以简单概况为以下4个步骤：

1. 提出零假设$H_0$以及对应的备选假设$H_1$(分为以下两种): \
     Non-directional(two tailed), e.g. $H_0:\mu=10,H_1:\mu_0\neq 10$;\
     Directional(one tailed), e.g. $H_0:\mu=10,H_1:\mu_0>10$(or $\mu_0<10$);\
2. 设定拒绝$H_0$的标准:\
     Set the significance level $\alpha$, e.g. 0.05;\
     Find the criteria for a decision: the critical value in z- or t-distribution;\
     Two tailed for non directional alternative hypothesis;\
     One tailed for directional alternative hypothesis;\
3. 计算测试统计数据:\
     $\sigma$已知：z-score;\
     $\sigma$未知：t-score;\
     $\sigma$未知但样本数据非常大：z-score。\
4. 决定是否拒绝零假设。\

One sample case for the mean

z-test

首先给一个图：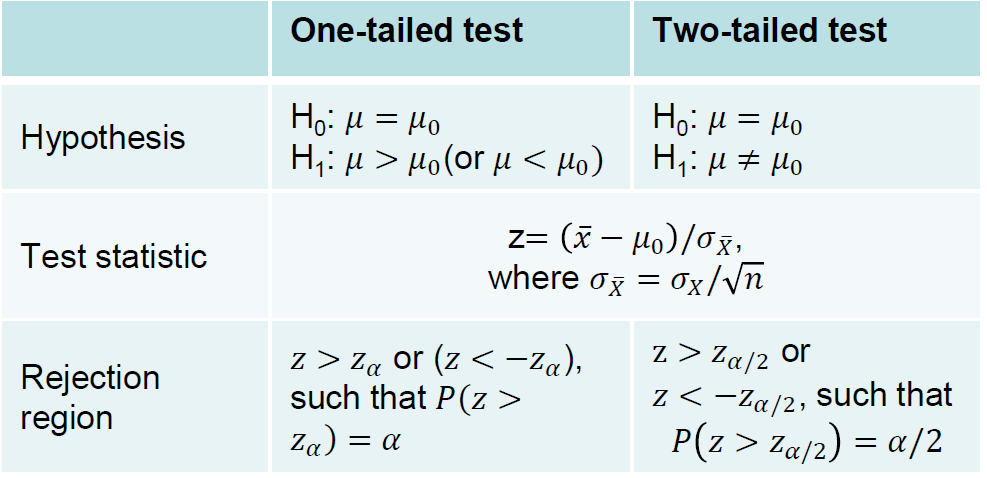
如果 $\overline{x}$ 是正态分布的话，则$z=\frac{\overline{x}-\mu_0}{\sigma_{\overline{x}}}$也是正态分布的（这里$\sigma_{\overline{x}}$是确定或已知的）。\
对于z检验，我们使用（累积）正态分布的表格来找出$z_{\alpha}$的值。\

一个例子

现用一个例子来说明z-test的步骤。\
以下20个样本是从已知标准差为5的正态分布中产生的。
现要检测该群体的均值是否大于6。\

1. Step 1: 设置假设：$H_0: \mu=6$ vs $H_1:\mu>6$;\
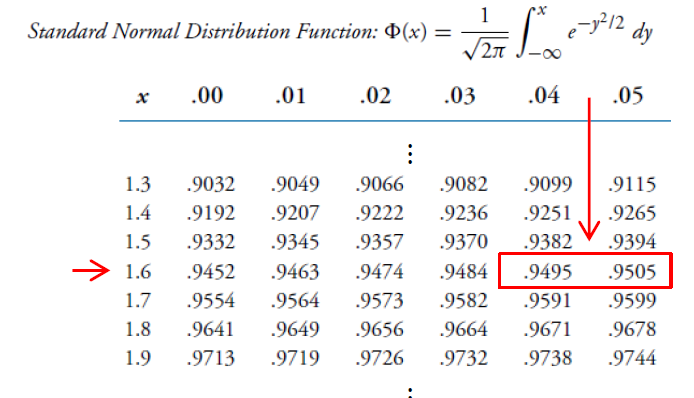
2. Step 2: 设置$\alpha$，比如说等于0.05，然后从下表中查出其临界值为：$z_{\alpha}=1.645$
3. Step 3: 计算样本的均值和标准差：
4. Step 4: 计算检测统计值： $$z=\frac{\overline{x}-\mu_0}{\sigma_{\overline{x}}}=\frac{5.572-6}{6.287/\sqrt{20}}=-0.304$$
5. Step 5: 做决策：由于$z < z_{\alpha}$，所以不拒绝零假设$H_0$。

t-test

依旧先给一个图：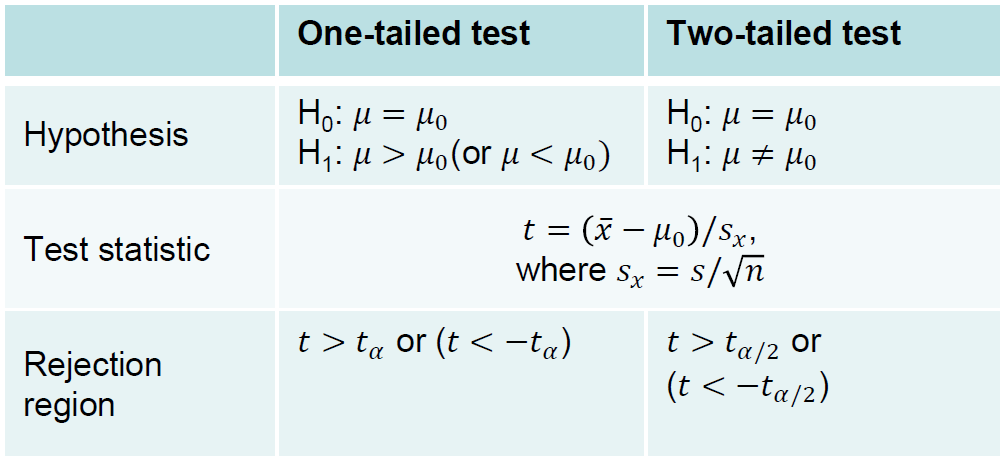
如果 $\overline{x}$ 是正态分布的话，则$t=\frac{\overline{x}-\mu_0}{s_x}$服从 t 分布（因为$s_x$是一个估计值，因此是另一个随机变量的输出）。\
这意味着，对于t检验，我们使用t分布的表格来找出𝑡的值。这个表比上面那个累积正态表复杂一丢丢，这里大概说一下怎么查。\
首先这个t分布表长这样：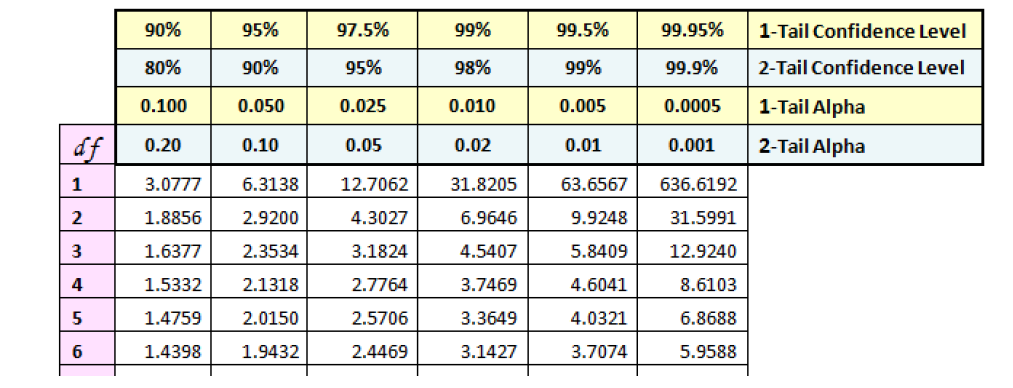
$t_{\alpha}$是基于$(n-1)$的，这个值称为自由度degree of freedom (df)。\
举个例子，比如说样本尺寸是7，单尾，则$t_{0.05}$为1.9432。\

Two sample case for the mean

上面的都是单样本的情况，这里开始介绍双样本，字面意思，就是两个样本（好像在说废话。。。。）。\
跟上面的区别还是有点大的，主要有以下两个方面：\

1. 假设不同，举两个例子：\
     女学生的GPA平均值是否要高于男学生；\
     在数据科学领域，女性的工资平均值是否高于男性；\
2. 情况不同：\
     样本独立：\
       方差已知；\
       方差未知：\
         总体方差未知但总体方差相等；\
         总体方差未知但总体方差不相等；\
         总体方差未知，也不知道它们的关系。\
     样本不独立。

以下对上面情况进行分别讨论。

样本独立，方差已知

方差已知的话就是z-test了。\
两总体均值差异为：$\overline{X}-\overline{Y}\sim \mathcal{N}(\mu_X-\mu_Y,\frac{\sigma_X^2}{n}+\frac{\sigma_Y^2}{m})$，其中$n,m$分别为$X,Y$两样本的大小。\
上面这个复杂的正态分布也可以写为：$\frac{\overline{X}-\overline{Y}-(\mu_X-\mu_Y)}{\sqrt{\frac{\sigma_X^2}{n}+\frac{\sigma_Y^2}{m}}}\sim \mathcal{N}(0,1)$，其实就是z-score。\
所以，当$H_0$为真时，即 $\mu_X-\mu_Y=0$ 时，z-test的统计量为：

$$z=\frac{\overline{X}-\overline{Y}}{\sqrt{\frac{\sigma_X^2}{n}+\frac{\sigma_Y^2}{m}}}$$

样本独立，方差未知

方差未知即是用t-test。

case 1：方差相等

方差相等即：$\mu_X^2=\mu_Y^2$。\
测试统计量为：$t=\frac{(\overline{x}-\overline{y})}{s_{\overline{x}-\overline{y}}}$，其中：

$$s_{\overline{x}-\overline{y}}=\sqrt{s^2(\frac{1}{n}+\frac{1}{m})}$$ $$s^2=\frac{\sum^n_{i=1}(x_i-\overline{x})^2+\sum^m_{j=1}(y_j-\overline{y})^2}{n+m-2}$$

或：

$$s^2=\frac{(n-1)s_x^2+(m-1)s_y^2}{n+m-2}$$ $$df=n+m-2$$

case 2：方差不相等

方差不相等即：$\mu_X^2\neq\mu_Y^2$。\
测试统计量为：$t=\frac{(\overline{x}-\overline{y})}{s_{\overline{x}-\overline{y}}}$，其中：

$$s_{\overline{x}-\overline{y}}=\sqrt{\frac{s_x^2}{n}+\frac{s_y^2}{m}}=\sqrt{s_{\overline{x}}^2+s_{\overline{y}}^2}$$ $$df = \frac{(s_{\overline{x}}^2+s_{\overline{y}}^2)^2}{\frac{(s_{\overline{x}}^2)^2}{n-1}+\frac{(s_{\overline{y}}^2)^2}{m-1}}$$

\
上面两个case中：\
$s_{\overline{x}}^2=\frac{s_x^2}{n};\quad s_{\overline{y}}^2=\frac{s_y^2}{m}; \quad s_x^2=\frac{\sum_{i=1}^n(x_i-\overline{x})^2}{n-1}; \quad s_y^2=\frac{\sum_{j=1}^m(y_j-\overline{y})^2}{m-1}$

case 3：方差关系未知

这里我们不知道 $\sigma_X^2$ 和 $\sigma_Y^2$ 相不相等，首先用 $F_{\max} test$ 检测方差的相等关系。\
这里简单补充下 $F_{\max}test$ 的相关内容。(这里仅补充这里需要用到的，更具体的看另一篇【F-test 方差分析】)。\

$F_{\max}test$

F 检测是一种方差差异性检测。\
测试统计量为：$F=\frac{s_x^2}{s_y^2}$，一般把较大的放分子上。\
F的临界值由以下三部分确定：\

1. 置信度$\alpha$；
2. 分子的自由度$df$；
3. 分母的自由度$df$。

根据这三个条件就可以查表了，由于F检测更多的是确定置信区间，所以要记得下面这个等式。

$$\frac{1}{F_{1-\frac{\alpha}{2}},m,n}=F_{\frac{\alpha}{2},n,m}$$

(注意这里 $m,n$ 的顺序)。\
决策依据是：\

1. 拒绝$H_0$: $F>F_{\frac{\alpha}{2}} \quad \rightarrow s_x^2 > s_y^2$；\
2. 拒绝$H_0$: $F< F_{1-\frac{\alpha}{2}} \quad \rightarrow s_x^2 < s_y^2$；\

置信区域如下：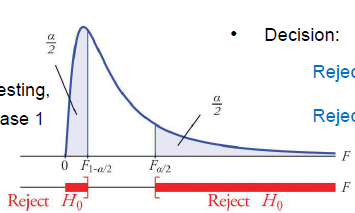
这里简单推导一下这个等式的由来。\
设$F\sim F(n,m)$，则$\frac{1}{F}\sim F(m,n)$。若

$$P\left\{ F>F_{1-\frac{\alpha}{2}}(n,m)\right\}=1-\frac{\alpha}{2}$$

即：

$$P\left\{ F< F_{1-\frac{\alpha}{2}}(n,m)\right\}=\frac{\alpha}{2}$$

则有：

$$P\left\{ \frac{1}{F}>\frac{1}{F_{1-\frac{\alpha}{2}}(n,m)}\right\}=\frac{\alpha}{2}$$

由于$\frac{1}{F}\sim F(m,n)$，转换一下就有：

$$P\left\{ \frac{1}{F}>{F_{\frac{\alpha}{2}}(m,n)}\right\}=\frac{\alpha}{2}$$

所以就得到了上面的等式：

$$\frac{1}{F_{1-\frac{\alpha}{2}},m,n}=F_{\frac{\alpha}{2},n,m}$$

回到 case 3\
运用F-test 进行方差检测，即：\

1. $H_0$: $\sigma_X^2=\sigma_Y^2$ 或 $\frac{\sigma_X^2}{\sigma_Y^2}=1$\

2. $H_1$: $\sigma_X^2 \neq \sigma_Y^2$ 或 $\frac{\sigma_X^2}{\sigma_Y^2}\neq 1$\
   (non-directional / two-tailed)

然后根据 F-test 的结果用上面 case 1 或者 case 2 的方法继续下去。

case 3 的一个例子

现在有两个导师A，B教同一门课，现在要探究哪个导数教的学生成绩更好。有以下数据：

	amount	average	Standard deviation
A	7	87	15
B	7	80	10

A导师说他更厉害，那我们现在就想检测他说的是不是真的。\
首先我们要检测两总体的方差是否相等：$H_0:\sigma_A^2=\sigma_B^2$ vs $H_1:\sigma_A^2\neq \sigma_B^2$; \

1. $F_{\max}$test：$F=\frac{s_A^2}{s_B^2}=\frac{15^2}{10^2}=2.25$；\
2. A, B 两类均有7个样本，则自由度均为：$df=n-1=7-1=6$；\
3. 选取 $\alpha$ 值，这里令 $\alpha = 0.05$，寻找寻找分子分母自由度均为6的边界值 $F_{cv}$；\
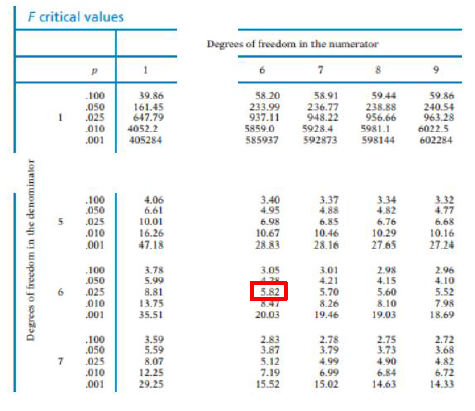
4. 从下面这个表中读取边界值：
   边界值 $F_{\alpha/2}=5.82$，即$F_{1-\alpha/2}=\frac{1}{5.82}=0.17$
5. 由于 $F$ 是位于0.17和5.82之间的，所以接受零假设，$\sigma_A^2=\sigma_B^2$。

我们得出了方差相等，现在继续往下，为验证导师A的话，做出如下新的假设：\

1. $H_0: \mu_A=\mu_B$ vs $H_1: \mu_A>\mu_B$，用case 1的方法;\
2. 计算：$s_{\overline{A}-\overline{B}}=\sqrt{\frac{(n-1)s_A^2+(m-1)s_B^2}{n+m-2}(\frac{1}{n}+\frac{1}{m})}=6.81$\
3. t 的统计量为：$t=\frac{87-80}{6.81}=1.03$，自由度为：7+7-2=12; \
4. 边界值为（one tailed）：$t_{0.05,12}=1.782$；\
5. 决策：由于 1.03 < 1.782，我们接受零假设，导师A的说法不靠谱。

另外多说一点，如果上面的数据，其它不变，但样本都变成700的话，就会发现导师A的说法是可信的，这个自行计算。\
值得注意的是，如果样本 n 很大，我们也可以用 z-test，700已经足够大了，有700个自由度的 t 分布已经很接近于正态分布了。\