卡尔曼滤波（Kalman Filter）

写在前面的说明

本文总结自B站博主DR_CAN，他是整个B站我最喜欢的博主没有之一，推荐大家直接去看他的视频，这篇当作学后的回顾，链接在这$\rightarrow$【传送门】。

引入 —— 递归算法

卡尔曼滤波器可看作是一种“Optimal Recursive Data Processing Algorithm”，即“最优的递归数字处理算法”。与滤波器相比它更像是一种观测器。
卡尔曼滤波器的应用非常广泛，尤其是导航中，这是因为现实生活中充满大量的不确定性，当我们描述一个系统的时候，这个不确定性主要体现在以下三个方面：

1. 不存在完美的数学模型；
2. 系统的挠动是不可控的，也很难建模；
3. 测量传感器存在误差。

举个例子：
当我们要测量一枚硬币的直径时，设第$k$次测量结果为$z_k$，假如三次测量分别为：

$$z_1=50.1mm$$ $$z_2=50.4mm$$ $$z_3=50.2mm$$

若要估计真实数据，很自然地，我们会用平均值来表示，即第$k$次的估计值$\hat{x}_k$为：

$$\begin{split} \hat{x}_k &= \frac{1}{k}(z_1+...+z_k)\\\\ &= \frac{1}{k}(z_1+...+z_{k-1})+\frac{1}{k}z_k\\\\ &= \frac{1}{k}\frac{k-1}{k-1}(z_1+...+z_{k-1})+\frac{1}{k}z_k \\\\ &=\frac{k-1}{k}\hat{x}_{k-1}+\frac{1}{k}z_k\\\\ &=\hat{x}_{k-1}-\frac{1}{k}\hat{x}_{k-1}+\frac{1}{k}z_k \end{split}$$

即是：

$$\hat{x}_k=\hat{x}_{k-1}+\frac{1}{k}(z_k-\hat{x}_{k-1})$$

由此可见，当$k$逐渐增加时，$\frac{1}{k}\rightarrow \infty$，也就是说$\hat{x}_k\rightarrow \hat{x}_{k-1}$。
用文字描述的话，就是说随着$k$的增加，之后测量结果也就不再重要了，也就是对前面的真实估计值已经非常有信心了。
相反，当$k$比较小时，$\frac{1}{k}$就会很大，也就是说此时$z_k$的作用会很大。
现在改写一下上面的式子为：

$$\hat{x}_k=\hat{x}_{k-1}+K_k(z_k-\hat{x}_{k-1})$$

在卡尔曼滤波器里，这个系数$K_k$就叫Kalman Gain，中文称为卡尔曼增益/因数。
由这个式子可以看出，跟马尔科夫链类似，当前估计值只与该次测量值以及上一次的估计值有关，这体现了一种递归的思想。
这里先对这个系数作简单的讨论。首先引入两个变量：

1. 估计误差：$e_{EST}$；
2. 测量误差：$e_{MEA}$。

卡尔曼增益就等于：

$$K_k=\frac{e_{EST_{k-1}}}{e_{EST_{k-1}}+e_{MEA_k}}$$

这个公式是卡尔曼滤波的核心公式，详细推导见后文。\
这里先简单讨论在$k$时刻两个变量的作用：

1. 当$e_{EST_{k-1}} \gg e_{MEA_k}$，即$k\rightarrow 1$时，$\hat{x}_k=\hat{x}_{k-1}+z_k-\hat{x}_{k-1}=z_{k}$；
2. 当$e_{EST_{k-1}} \ll e_{MEA_k}$，即$k\rightarrow 0$时，$\hat{x}_k=\hat{x}_{k-1}$。

运用卡尔曼滤波器，真实估计值就可以表示为以下三个步骤：

1. Step 1：计算卡尔曼增益：$K_k=\frac{e_{EST_{k-1}}}{e_{EST_{k-1}}+e_{MEA_k}}$；
2. Step 2：计算当前估计值$\hat{x}_k=\hat{x}_{k-1}+K_k(z_k-\hat{x}_{k-1})$；
3. Step 3：更新$e_{EST_k}=(1-K_k)e_{EST_{k-1}}$（这个式子后面推导）。

这里举个例子说明上面三个步骤：
假设我们要测量一个长度是$50mm$的物体，第0次的估计值，也就是相当于先验吧，是$\hat{x}_0=40mm$，第0次估计误差为$e_{EST_0}=5mm$，第一次测量为$z_1=51mm$，测量误差一直为$e_{MEA_k}=3mm$。
填入起始值，如下表：

$k$	$z_k$	$e_{MEA_k}$	$\hat{x}_k$	$K_k$	$e_{EST_k}$
0			40		5
1	51	3
2
3

借助上面三个步骤：
$k=1$时：

$$K_k=\frac{5}{5+3}=0.625$$ $$\hat{x}_k=40+0.625(51-40)=46.875$$ $$e_{EST}=(1-0.625)\times 5 = 1.875$$

然后$k=2$时，设此次测量值为$z_2=48$，重复上面的步骤，就可以填满表格了。如下：

$k$	$z_k$	$e_{MEA_k}$	$\hat{x}_k$	$K_k$	$e_{EST_k}$
0			40		5
1	51	3	46.88	0.625	1.875
2	48	3	47.31	0.385	1.154
3	47	3	47.22	0.278	0.833

这样不断下去，最后这个真实估计值会收敛于$50mm$。
借用博主视频里的数值结果图片，其表现如下：

其中蓝色线表示测量值，红色线表示估计值。

数据融合，协方差矩阵，状态空间方程

这部分是复习基础知识，可跳过。

数据融合

简单讲，就是从多个测量数据中找到一个最优的。
举个例子，我们在称量一个物体的时候，两次称量结果如下：

$$z_1=30g, \quad \sigma_1=2g$$ $$z_2=32g, \quad \sigma_2=4g$$

根据正态分布的性质，对于第一个测量结果，真实值落在区间[28,32]的概率是68.4%；对第二个测量结果，真实值落在区间[28,36]的概率是68.4%，如果这时候要我们估计真实值的话，我们会把真实值估计在区间[30,32]之间，而且由于第一个测量标准差较小，所以真实值会更靠近于30。
如果要我们在数学上得到一个比较准确的值，就可以用上面递归的方法，写出如下等式：

$$\hat{z}=z_1+K(z_2-z_1)$$

其中 $K\in [0,1]$，当$K=0$时，$\hat{z}=z_1$；当$K=1$时，$\hat{z}=z_2$。\
现在我们要求$K$，使得 $\sigma_{\hat{z}}$ 最小，即是要 $Var(\hat{z})$ 最小。
而这个方差我们可以写成：

$$\sigma_{\hat{z}}^2=Var(z_1+K(z_2-z_1))=Var((1-K)z_1+Kz_2)$$

由于括号里的两项 $(1-K)z_1$ 和 $Kz_2$ 相互独立(毕竟是两个不同的称，称量结果肯定不会相互影响)，根据方差的性质，上面式子可以继续往下写：

$$Var((1-K)z_1+Kz_2)=Var((1-K)z_1)+Var(Kz_2)=(1-K)^2Var(z_1)+K^2Var(z_2)$$

将上面两个方差代入得：

$$(1-K)^2Var(z_1)+K^2Var(z_2)=(1-K)^2\sigma_1^2+K^2\sigma_2^2$$

也就是说：

$$\sigma_{\hat{z}}^2=(1-K)^2\sigma_1^2+K^2\sigma_2^2$$

现在要求最小值，所以就是对$K$进行求导：

$$\frac{d\sigma_{\hat{z}}^2}{dK}=0$$

(中间过程自行计算)\
最后求出$K$的值为：

$$K=\frac{\sigma_1^2}{\sigma_1^2+\sigma_2^2}=0.2$$

把$K$代入上面式子，其最佳估计值为：

$$\hat{z}=z_1+K(z_2-z_1)=30+0.2(32-30)=30.4$$

其方差为：

$$\sigma_{\hat{z}}^2=(1-0.2)^22^2+0.2^24^2=3.2$$

标准差为：$\sqrt{3.2}=1.79$
这个计算过程就是数据融合。

协方差矩阵

协方差矩阵是将矩阵，协方差在一个矩阵中表示出来，表明变量空间的联动关系。比如说下面这个表格：

名字	身高$(x)$	体重$(y)$	年龄$(z)$
A	179	74	33
B	187	80	31
C	175	71	28
均值	180.3	75	30.7

计算出变量$x,y,z$的方差为：

$$\sigma_x^2=24.89,\quad \sigma_y^2=14,\quad\sigma_z^2=4.22$$

计算协方差为：

$$\begin{aligned} \sigma_x\sigma_y &= \frac{1}{3}((179-180.3)(74-75)+(187-180.3)(80-75)+(175-180.3)(71-75))\\ &= 18.7=\sigma_y\sigma_x \end{aligned}$$

同理：

$$\sigma_x\sigma_z=4.4=\sigma_z\sigma_x, \quad \sigma_y\sigma_z=3.3=\sigma_z\sigma_y$$

(协方差矩阵是对称矩阵。)
协方差矩阵形式如下：

$$\left[ \begin{matrix} \sigma_x^2 & \sigma_{x,y} & \sigma_{x,z} \\ \sigma_{y,x} & \sigma_y^2 & \sigma_{y,z} \\ \sigma_{z,x} & \sigma_{z,y} & \sigma_z^2 \end{matrix} \right]$$

代入数据：

$$\left[ \begin{matrix} 24.89 & 18.7 & 4.4 \\ 18.7 & 14 & 3.3 \\ 4.4 & 3.3 & 4.22 \end{matrix} \right]$$

矩阵计算的方法
在写代码的时候，用矩阵计算方法计算协方差明显更容易书写，其形式如下：\
过渡矩阵：

$$a= \left[ \begin{matrix} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \end{matrix} \right] - \frac{1}{3} \left[ \begin{matrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{matrix} \right] \left[ \begin{matrix} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \end{matrix} \right]$$

协方差矩阵：

$$P=\frac{1}{3}a^Ta$$

现在我们观察上面得出的那个协方差矩阵，先看对角线，前两个数字都很大（其实第三个数字不应该这么小的，但毕竟只取了三个数据，偶然性太大），表明数据波动是比较大的，说明身高体重在这个群体里影响不大；接着看其它数据，比如这个18.7，说明身高跟体重是成正比的，且相关性较大，也符合常理；然后再看看4.4，说明身高跟年龄关系不大，也对，到一定年龄身高跟年龄关系就不大了……\

状态空间方程

比如说对于一个弹簧阻尼系统：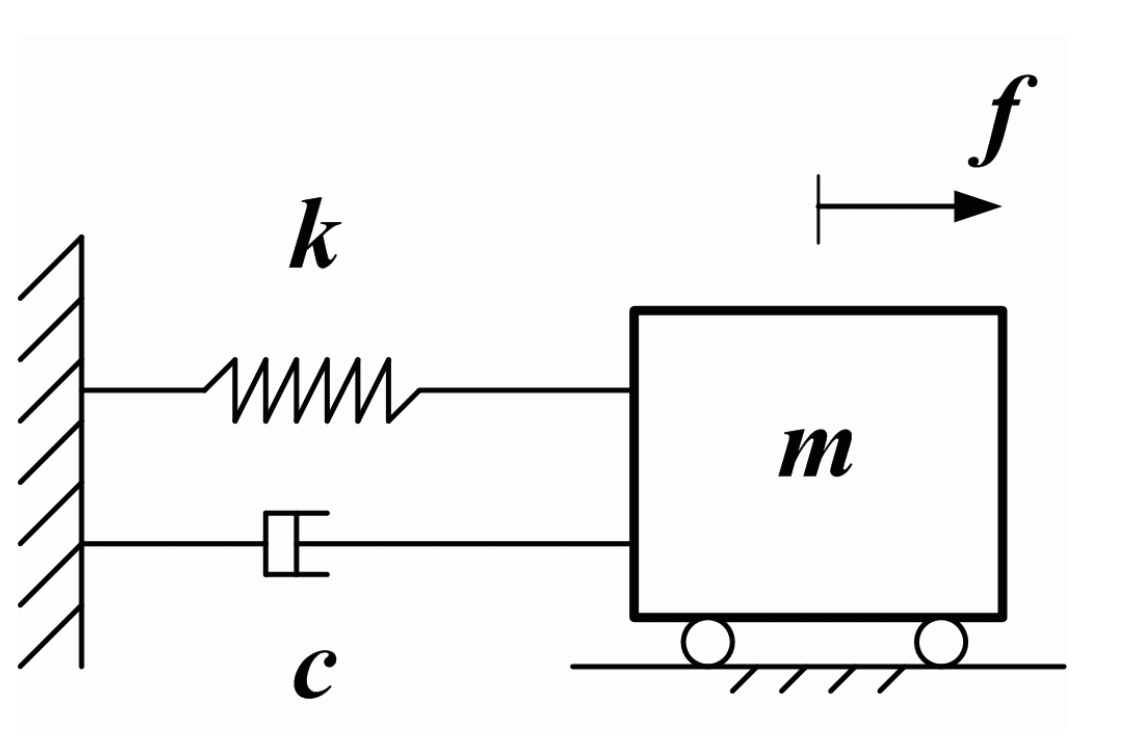
我们可以很容易写出如下微分方程($x$为位移)：

$$m\ddot{x}+c\dot{x}+kx=F$$

状态量为：

$$x_1=x;\quad x_2=\dot{x}$$

观测量为：

$$z_1=x=x_1;位置\quad z_2=\dot{x}=x_2速度$$

设$F$为输入值，等于$u$。\
写成一阶微分矩阵形式如下：

$$\left[ \begin{matrix} \dot{x_1} \\ \dot{x_2} \end{matrix} \right] = \left[ \begin{matrix} 0 & 1 \\ -\frac{k}{m} & -\frac{c}{m} \end{matrix} \right] \left[ \begin{matrix} x_1 \\ x_2 \end{matrix} \right] + \left[ \begin{matrix} 0 \\ \frac{1}{m} \end{matrix} \right] u$$

观测矩阵为：

$$\left[ \begin{matrix} z_1 \\ z_2 \end{matrix} \right] = \left[ \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \right] \left[ \begin{matrix} x_1 \\ x_2 \end{matrix} \right]$$

以上两个矩阵表达式就是状态空间表达式，归纳一下可以写为：

$$\dot{X}_t=AX_t+Bu_t$$ $$Z_t=HX_t$$

这是一种连续的表达式，左边$X$是对时间求导。\
写成离散形式为：

$$X_k=AX_{k-1}+Bu_{k-1}$$ $$Z_k=HX_k$$

其下标$k.k+1,k+2…$为时间单位，即是采样。\
在实际生活中到处充满着不确定性，上面那个离散的状态空间表达式可以写为：

$$X_k=AX_{k-1}+Bu_{k-1}+w_{k-1}$$ $$Z_k=HX_k+v_k$$

其中$w_{k-1}$为过程噪音，$v_k$为测量噪音。\
根据这些如何去估计一个$\hat{X}_k$呢？这就是卡尔曼滤波器要解决的问题。

卡尔曼增益的数学推导

在一开始我们用了卡尔曼增益，但却没有解释为什么这个增益是这种形式，这部分就是对它的推导。\
将上面那个离散情况下带噪音的状态空间方程写下来如下：

$$X_k=AX_{k-1}+Bu_{k-1}+w_{k-1}$$ $$Z_k=HX_k+v_k$$

两个方程的噪音部分是我们不可测的，但在自然界中我们可以把这噪声假设成正态分布(why? 只能说自然界就是这么神奇)。所以我们可以把过程噪音写成：

$$P(w) \sim (0,Q)$$

这里0是期望，$Q$是协方差矩阵。这个$Q$可以用下面的式子计算：

$$Q=E[ww^T]$$

举个例子，假如现在$X_k$由两部分组成，即是：

$$X_k= \left[ \begin{matrix} x_1 \\ x_2 \end{matrix} \right]$$

则对应的过程噪音就是：

$$\left[ \begin{matrix} w_1 \\ w_2 \end{matrix} \right]$$

这个噪音的协方差矩阵为：

$$E[ \left[ \begin{matrix} w_1 \\ w_2 \end{matrix} \right] \left[ \begin{matrix} w_1 & w_2 \end{matrix} \right] ] = \left[ \begin{matrix} E[w_1^2] & E[w_1w_2] \\ E[w_2w_1] & E[w_2^2] \end{matrix} \right]$$

另外，对于方差我们有：

$$Var(x)=E(x^2)-E^2(x)$$

在这里噪音的期望为0，所以：$Var(x)=E(x^2)$，上面的矩阵可以写为：\

$$E[ \left[ \begin{matrix} w_1 \\ w_2 \end{matrix} \right] \left[ \begin{matrix} w_1 & w_2 \end{matrix} \right] ] = \left[ \begin{matrix} \sigma_{w_1}^2 & \sigma_{w_1,w_2} \\ \sigma_{w_2,w_1} & \sigma_{w_2}^2 \end{matrix} \right]$$

噪音的协方差矩阵就出来了，所以这个式子：

$$Q=E[ww^T]$$

是正确的。
同理，对于测量噪音$v_k$，也是一样的：

$$p(v)\sim (0,R)$$

$R$是协方差矩阵，同样用上面的方法也可以计算。\
在实际建模中，这两个噪音我们是无法建模出来的，我们能计算的只是下面这个东西：

$$X_k^-=AX_{k-1}+Bu_{k-1} \tag{1}$$

少了噪音那项，像这种我们直接计算出来的我们称为先验估计值，表示为估计值上面带个减号。\
对于测量部分，我们有：

$$\hat{X}_{k,mea}=H^{-1}Z_{k} \tag{2}$$

这是测量估计值。\
现在我们有两个结果，分别是先验估计值和测量估计值，但这两个都不具备噪声的影响，都是不准确的，然后卡尔曼滤波器的作用就出来了：通过两个不太准确的结果得出一个比较准确的结果。\
根据上面【数据融合】那部分的知识，后验估计值(就是我们想要的)可以写成：

$$\hat{X}_k=\hat{X}_{k}^-+G(H^{-1}Z_k-\hat{X}_{k}^-)$$

这里$G\in [0,1]$，当$G=0$时，$\hat{X}_k=\hat{X}_{k}^-$，表明更相信计算的结果，也就是先验估计值；如果$G=1$，$\hat{X}_k=H^{-1}Z_{k}$，表明更相信测量的结果。\
在其它地方上面的式子会写成这样：

$$\hat{X}_k=\hat{X}_k^-+K_k(Z_k-H\hat{X}_{k}^-)$$

这里的$G=K_kH$，其实一个一声，但要注意的是，这里的$K\in[0,H^{-1}]$。\
现在我们要做的就是寻找这个$K_k$，使得$\hat{X}_k$趋近于$X_{k}$。这里我们定义一个误差：

$$e_k=X_k-\hat{X}_k$$

这里的误差$e_k$也是一个符合正态分布的矩阵：$P(e_{k})\sim (0,P)$(这个应该很容易理解)，依旧按照上面的方法求这个协方差矩阵：

$$P=E[ee^T]= \left[ \begin{matrix} \sigma_{e_1}^2 & \sigma_{e_1,e_2} \\ \sigma_{e_2,e_1} & \sigma_{e_2}^2 \end{matrix} \right]$$

我们这个估计值$\hat{X}_k$越接近于实际值，就说明这个误差的方差越小，也就说明越接近于0。现在问题就变成了我们需要选取适当的$K_k$，使协方差矩阵的迹最小，即$tr(P)$最小。(元素分开考虑，所以是对角线)。

$$tr(P)=\sigma_{e_1}^2+\sigma_{e_2}^2$$

现在我们首先把协方差矩阵求出来，对于误差有：

$$e_k=X_k-\hat{X}_k$$

将其代入协方差矩阵的式子得：

$$\begin{aligned} P &= E[ee^T]\\ &=E[(X_k-\hat{X}_k)(X_k-\hat{X}_{k})^T] \end{aligned}$$

将

$$\hat{X}_k=\hat{X}_k^-+K_k(Z_k-H\hat{X}_{k}^-)$$ $$Z_k=HX_k+v_k$$

代入得：

$$\begin{aligned} X_k-\hat{X}_k &= (X_k-\hat{X}_{k}^-)-K_kH(X_k-\hat{X}_{k}^-)-K_kv_k \\ &=(I-K_kH)(X_k-\hat{X}_{k}^-)-K_kv_k \end{aligned}$$

定义先验误差 $e_k^-=(X_k-\hat{X}_{k}^-)$。\
所以上面的协方差矩阵可以写为：

$$\begin{aligned} P_k &= E[ee^T]\\ &= E[(X_k-\hat{X}_k)(X_k-\hat{X}_{k})^T]\\ &= E[[(I-K_kH)e_k^--K_kv_k][(I-K_kH)e_k^--K_kv_k]^T]\\ &= E[(I-K_kH)e_k^-{e_k^-}^T(I-K_kH)^T]-E[(I-K_kH)e_k^-v_k^TK_k^T] -E[K_kv_k{e_k^-}^T(I-K_kH)^T]+E[K_kv_kv_k^TK_k^T] \end{aligned}$$

由于$(I-K_kH)$是常数，且对于独立的$A,B$，有$E(AB)=E(A)E(B)$，$E(e_K^-)=E(v_k^T)=0$，所以上式的中间两项为0。上式可以继续化简：

$$\begin{aligned} P_k &= E[ee^T]\\ &= E[(X_k-\hat{X}_k)(X_k-\hat{X}_{k})^T]\\ &= E[[(I-K_kH)e_k^--K_kv_k][(I-K_kH)e_k^--K_kv_k]^T]\\ &= E[(I-K_kH)e_k^-{e_k^-}^T(I-K_kH)^T]-E[(I-K_kH)e_k^-v_k^TK_k^T] -E[K_kv_k{e_k^-}^T(I-K_kH)^T]+E[K_kv_kv_k^TK_k^T]\\ &= (I-K_kH)E[(e_k^-{e_k^-}^T)](I-K_kH)^T+K_kE[v_kv_k^T]K_k^T \end{aligned}$$

由于$E[(e_k^-{e_k^-}^T)]$为先验误差的协方差矩阵$P_k^-$，$R=E[v_kv_k^T]$上面等式就可以继续化简：

$$\begin{aligned} P_k &= E[ee^T]\\ &= E[(X_k-\hat{X}_k)(X_k-\hat{X}_{k})^T]\\ &= E[[(I-K_kH)e_k^--K_kv_k][(I-K_kH)e_k^--K_kv_k]^T]\\ &= E[(I-K_kH)e_k^-{e_k^-}^T(I-K_kH)^T]-E[(I-K_kH)e_k^-v_k^TK_k^T] -E[K_kv_k{e_k^-}^T(I-K_kH)^T]+E[K_kv_kv_k^TK_k^T]\\ &= (I-K_kH)E[(e_k^-{e_k^-}^T)](I-K_kH)^T+K_kE[v_kv_k^T]K_k^T\\ &=(P_k^--K_kHP_k^-)(I-H^TK_k^T)+K_kRK_k^T\\ &=P_k^--K_kHP_k^--P_k^-H^TK_k^T+K_kHP_k^-H^TK_k^T+K_kRK_k^T \end{aligned}$$

现在就求出这个协方差矩阵了，接下来是求迹。我们看右边第三项，对其转置：

$$((P_k^-H^T)K_k^T)^T=K_k(P_k^-H^T)^T=K_kH{P_k^-}^T$$

也就是说，第三项的转置等于第二项，所以第三项的迹与第二项相同。所以协方差矩阵的迹为：

$$tr(P_k)=tr(P_k^-)-2tr(K_kHP_k^-)+tr(K_kHP_k^-H^TK_k^T)+tr(K_kRK_k^T)$$

现在要求迹最小时对应的$K_k$，即是求导等于0。\
这里先说个东西：

$$\frac{dtr(AB)}{dA}=B^T$$ $$\frac{d(ABA^T)}{dA}=2AB$$

(这个自己验证)\
所以：

$$\frac{dtr(P_k)}{dK_k}=0-2(HP_k^-)^T+2K_kHP_k^-H^T+2K_kR=0$$

即：

$$-P_k^-H^T+K_k(HP_k^-H^T+R)=0$$ $$K_k=\frac{P_k^-H^T}{HP_k^-H^T+R}$$

这就是卡尔曼滤波器最核心的公式，分析一下，当$R$特别大时，即测量噪声特别大时，$K_k$就趋近于0，此时估计值$\hat{X}_k$就等于先验估计$\hat{X}_{k}^-$，我们就更愿意相信计算的先验估计；当$R$很小时，$K_k$就趋近于$H^{-1}$，估计值就等于测量估计。

误差协方差矩阵

上面我们得出了卡尔曼增益的表达式：

$$K_k=\frac{P_k^-H^T}{HP_k^-H^T+R}$$

在这个表达式中$P_k^-$我们还不知道，这部分就是对这个的推导。\
我们已知：

$$P_k^-=E[e_k^--{e_k^-}^T]$$ $$\begin{aligned} e_k^- &=X_k-\hat{X}_k^-\\ &= AX_{k-1}+Bu_{k-1}+w_{k-1}-A\hat{X}_{k-1}-Bu_{k-1}\\ &= A(X_{k-1}-\hat{X}_{k-1})+w_{k-1}\\ &= Ae_{k-1}+w_{k-1} \end{aligned}$$

代入上面的协方差矩阵：

$$\begin{aligned} P_k^- &=E[e_k^--{e_k^-}^T]\\ &= E[(Ae_{k-1}+w_{k-1})((Ae_{k-1})^T+(w_{k-1})^T)]\\ &= E[Ae_{k-1}e_{k-1}^TA^T]+E[Ae_{k-1}w_{k-1}^T]+E[w_{k-1}e_{k-1}^TA^T]+E[w_{k-1}w_{k-1}^T] \end{aligned}$$

这里，由于$e_{k-1}$和$w_{k-1}$是相互独立的（$e_{k-1}$与$w_{k-1}$无关而与$w_{k-2}$有关），所以相乘的期望等于期望的相乘，都等于0，上面式子中间两项等于0，可以写为：

$$\begin{aligned} P_k^- &=E[e_k^--{e_k^-}^T]\\ &= E[(Ae_{k-1}+w_{k-1})((Ae_{k-1})^T+(w_{k-1})^T)]\\ &= E[Ae_{k-1}e_{k-1}^TA^T]+E[Ae_{k-1}w_{k-1}^T]+E[w_{k-1}e_{k-1}^TA^T]+E[w_{k-1}w_{k-1}^T]\\ &= AE[e_{k-1}e_{k-1}^T]+E[w_{k-1}w_{k-1}^T]\\ &= AP_{k-1}A^T+Q \end{aligned}$$

至此，就可以用卡尔曼滤波器来估计状态变量的值了。这个过程分为两步：

预测：\
 计算先验：$\hat{X}_k^-=A\hat{X}_{k-1}+Bu_{k-1} \tag{1}$\
 先验误差协方差：$P_k^-=AP_{k-1}A^T+Q \tag{2}$

校正：\
 卡尔曼增益：

$$K_k=\frac{P_k^-H^T}{HP_k^-H^T+R} \tag{3}$$

 后验估计：

$$\hat{X}_k=\hat{X}_{k}^-+K_k(Z_k-H\hat{X}_k^-) \tag{4}$$

由于在预测中用了上一次的误差协方差，所以要更新这个参数，在上一部分我们得出了：

$$P_k=P_k^--K_kHP_k^--P_k^-H^TK_k^T+K_kHP_k^-H^TK_k^T+K_kRK_k^T$$

将算出的$K_k$代入得：

$$P_k=P_k^--K_kHP_k^-=(I-K_kH)P_k^- \tag{5}$$

上面公式(1) — (5)就是卡尔曼滤波器最重要的5个公式了，在最开始的时候我们要初始化$\hat{X}_0$ 和 $P_{0}$。