李群和李代数

1. 群的定义

群(Group)是一种集合加上一种运算的代数结构，以A表示集合，“·”表示运算，则群一般写作 G(A, ·)。群要求满足以下四个条件：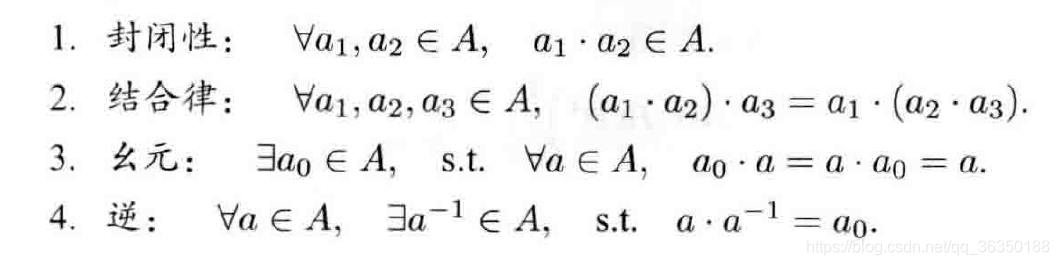


举个例子，旋转矩阵和乘法可以构成旋转矩阵群，因为其满足：

1). 旋转矩阵相乘后仍是旋转矩阵；
2). 矩阵乘法满足结合律；
3). 幺元为单位矩阵，也属旋转矩阵；
4). 旋转矩阵的逆也为旋转矩阵，且相乘为单位矩阵。

常见的群有：

2. 李群

李群是指拥有(连续)光滑性质的群，比如上面提到的旋转矩阵群，因其能在空间中连续旋转，变换矩阵群也是李群（就是在旋转过程中加上平移）。

3. 李代数的引入

直观的导出

在视觉SLAM中，我们需要做的就是不断计算相机的位姿和构建地图（其中的相机位姿表现在其变换矩阵T），但由于干扰的存在，我们无法准确获得所需要的信息，所以我们转而求其最小误差。\
现假设我们有N个三维点p和对应的观测值z，那么我们的目标就是寻找一个最佳的位姿T，使得整体误差最小化，也就是求：

要求解上面的方程，即是要求目标函数J对T的导数，但由于T所在的变换矩阵群（下面用SO(3)空间表示）对加法不封闭，无法直接求取，所以我们需要引入一个新的量，通过对该量的计算间接获得对变换矩阵T的求导，这个引入的量就是李代数。

数学层面的导出

（之后的部分《视觉SLAM 十四讲》里写得已经很精炼很清楚了，这里大概重述一遍以加深印象，也方便以后的查询）

先给一个结论：李代数对应李群的正切空间，描述了李群的局部导数。

这里用旋转矩阵群SO(3)为例：\
我们知道旋转矩阵满足以下关系：$RR^{T}=I$
然后引入时间变量$t$变为时间的函数$R(t)$，即是有：$R(t)R(t)^{T}=I$
对两边求导得到：$\dot{R}(t)R(t)^{T}+\dot{R}(t)^{T}R(t)=0$
整理得：$\dot{R}(t)R(t)^{T}=-(\dot{R}(t)R(t)^{T})^{T}$
可见，$\dot{R}(t)R(t)^{T}$是一个反对称矩阵。用符号$^{\land}$表示反对称矩阵，设：$a=\begin{bmatrix} a_{1} \\ a_{2} \\ a_{3} \end{bmatrix}$
则$a^{\land}$为：$a^{\land}=A=\begin{bmatrix} 0 & -a_{3} & a_{2} \\ a_{3} & 0 & -a_{1} \\ -a_{2} & a_{1} & 0 \end{bmatrix}$
同理：$A^{\vee}=a$
我们设一个三维向量$\phi(t)\in\Re^{3}$与反对称矩阵$\dot{R}(t)R(t)^{T}$对应，即：$\dot{R}(t)R(t)^{T}=\phi(t)^{\land}$
等式两边右乘$R(t)$，由于$R$为正交阵，得：$\dot{R}(t)=\phi(t)^{\land}R(t)=\begin{bmatrix}0 & -\phi_{3} & \phi_{2}\\\phi_{3}&0&-\phi_{1}\\-\phi_{2}&\phi_{1}&0\end{bmatrix}R(t)$
由此可见，每对$R$求一次导数，只需左乘一个$\phi^{\land}(t)$即可。\
当$t=0$时，设此时$R(0)=I$，把$R(t)$在$t=0$附近进行一阶泰勒展开得：$R(t)\approx R(t_{0})+\dot{R}(t_{0})(t-t_{0})=I+\phi(t_{0})^{\land}(t)$
可见，$\phi$反映了$R$的导数性质，所以称它为SO(3)原点附近的正切空间。同时在$t_{0}$附近设$\phi$保持为常数$\phi(t_{0})=\phi_{0}$，故有：$\dot{R}(t)=\phi(t_{0})^{\land}R(t)=\phi_{0}^{\land}R(t)$
这是一个关于$R$的微分方程，且初始值$R(0)=I$，解得：$R(t)=exp(\phi_{0}^{\land}t)$
表明，旋转矩阵可由$exp(\phi_{0}^{\land}t)$计算出来，给定某时刻的$R$我们就能求得一个$\phi$，它描述$R$在局部的导数关系，这个$\phi$正是对应到SO(3)上的李代数so(3)。

4. 李代数的定义

每个李群都有其对应的李代数，一般李代数的定义如下：

二元运算[,]称为李括号，表达两元素的差异。举个例子，三维向量$\Re^{3}$的叉积就是一种李括号，因此$g=(\Re^{3},\Re,\times)$构成了一个李代数。

5. 李代数so(3)

由上面的结果可得，三维向量$\phi$为李群SO(3)所对应的，定义在$\Re^{3}$上的李代数，每个$\phi$对应一个反对称矩阵：$\Phi=\phi(t)^{\land}R(t)=\begin{bmatrix}0 & -\phi_{3} & \phi_{2}\\\phi_{3}&0&-\phi_{1}\\-\phi_{2}&\phi_{1}&0\end{bmatrix}\in \Re^{3\times3}$
两个向量$\phi_{1},\phi_{2}$的李括号为：$[\phi_{1},\phi_{2}]=(\Phi_{1}\Phi_{2}-\Phi_{2}\Phi_{1})^{\vee}$
它与SO(3)的关系由指数映射指定：$R=exp(\phi^{\land})$

6. 李代数se(3)

SE(3)对应的李代数se(3)与so(3)类似，但其定义在$\Re^{6}$空间中，如下：

我们把每个se(3)的元素记作$\xi$，表示一个六维向量，前三维表平移，但不同于变换矩阵的平移，记作$\rho$，后三维表旋转，记作$\phi$，其实就是上面提到的so(3)元素。se(3)表示如下（注：这里的$\land$不再表示反对称矩阵，而是表示六维向量向四维矩阵的转换）：

$$\xi^{\land}=\begin{bmatrix}\phi^{\land}&\rho\\0^{T}&0\end{bmatrix}$$

(注：$\land$和$\vee$这里表示“从向量到矩阵”和“从矩阵到向量”，se(3)可理解成：由平移加上一个so(3)元素构成的向量)\
其李括号为：$[\xi_{1},\xi_{2}]=(\xi^{\land}_{1}\xi^{\land}_{2}-\xi^{\land}_{2}\xi^{\land}_{1})^{\vee}$

7. 指数与对数映射

矩阵的指数如$exp(\phi^{\land})$在李群李代数中称为指数映射。

关于so(3)的映射

那么如何计算$exp(\phi^{\land})$呢？首先，任何矩阵$A$的指数都可以表示成一个泰勒展开，但只有收敛的情况下才会有结果，结果如下：$exp(A)=\sum_{n=0}^{\infty}\frac{1}{n!}A^{n}$
即是对so(3)的元素有：$exp(\phi^{\land})=\sum_{n=0}^{\infty}\frac{1}{n!}(\phi^{\land})^{n}$
但要计算这个太复杂，因为有无穷次幂。所以一般情况下我们用下面的方法：$\phi$是一个三维向量，我们定义其模长和方向，分别记为$\theta$和$a$，写作$\phi=\theta a$，这里$a$的模长为1.即: $||a||=1$:

$$a = [a_{1}, a_{2}, a_{3}]^{T}$$ $$a^{2}_{1}+a^{2}_{2}+a^{2}_{3}=1$$

对于$a^{\land}$有以下性质：

图里的两个式子提供了处理高阶$a^{\land}$的方法，所以其指数映射可写成一个神奇的形式：（最好自己写一遍）


这个式子与罗德里格斯公式如出一辙。

这里简单回顾下罗德里格斯公式（旋转向量到旋转矩阵的转化）：

$$R=cos\theta I+(1-cos\theta)nn^{T}+sin\theta n^{\land}$$ 两边取迹（即是求矩阵对角线元素之和）：$$tr(R)=cos\theta tr(I)+(1-cos\theta)tr(nn^{T})+sin\theta tr(n^{\land})\\=3cos\theta+(1-cos\theta)=1+2cos\theta$$

所以角度为：

$$\theta=arc cos\frac{tr(R)-1}{2}$$

这表明，so(3)实际就是由旋转向量组成的空间，而指数映射即是罗德里格斯公式。\
反之，通过对数映射也可以将SO(3)的元素对应到so(3)中：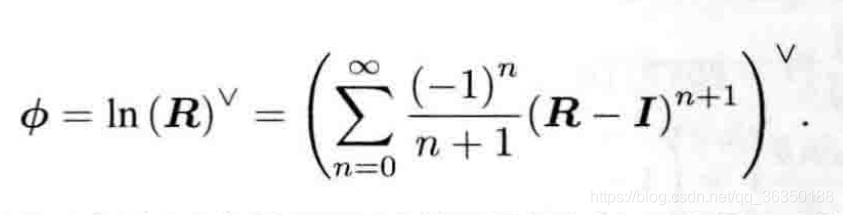

对这个式子的求解也没必要用泰勒展开，而是可以通过迹的性质分别求解转角和转轴（上面回顾罗德里格斯公式的时候已经一起列出来了）。\
最后需要提一下：每个SO(3)中的元素都可以找到一个so(3)元素与之对应，但一个so(3)元素却可能有多个SO(3)中的元素，直观一点理解的话：比如旋转360度会对应一个周期。

关于se(3)的映射（待补充。。。）

与so(3)的过程类似，所以这里主要给结论（这个过程没具体算，之后补上。）。\
se(3)的指数映射形式如下：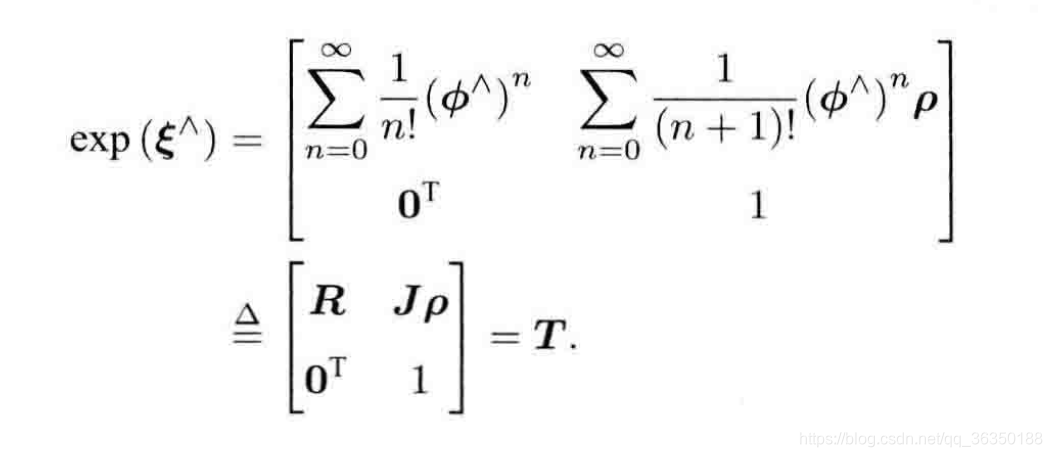

同样令$\phi=\theta a$，$a$为单位向量，则：

从结果来看，$\xi$的指数映射左上角的$R$就是上面的SO(3)，与se(3)中的旋转部分$\phi$对应，而右上角的$J$由上面图里的推导给出，即：

映射表*

这里给出SO(3), SE(3), so(3), se(3)的对应映射表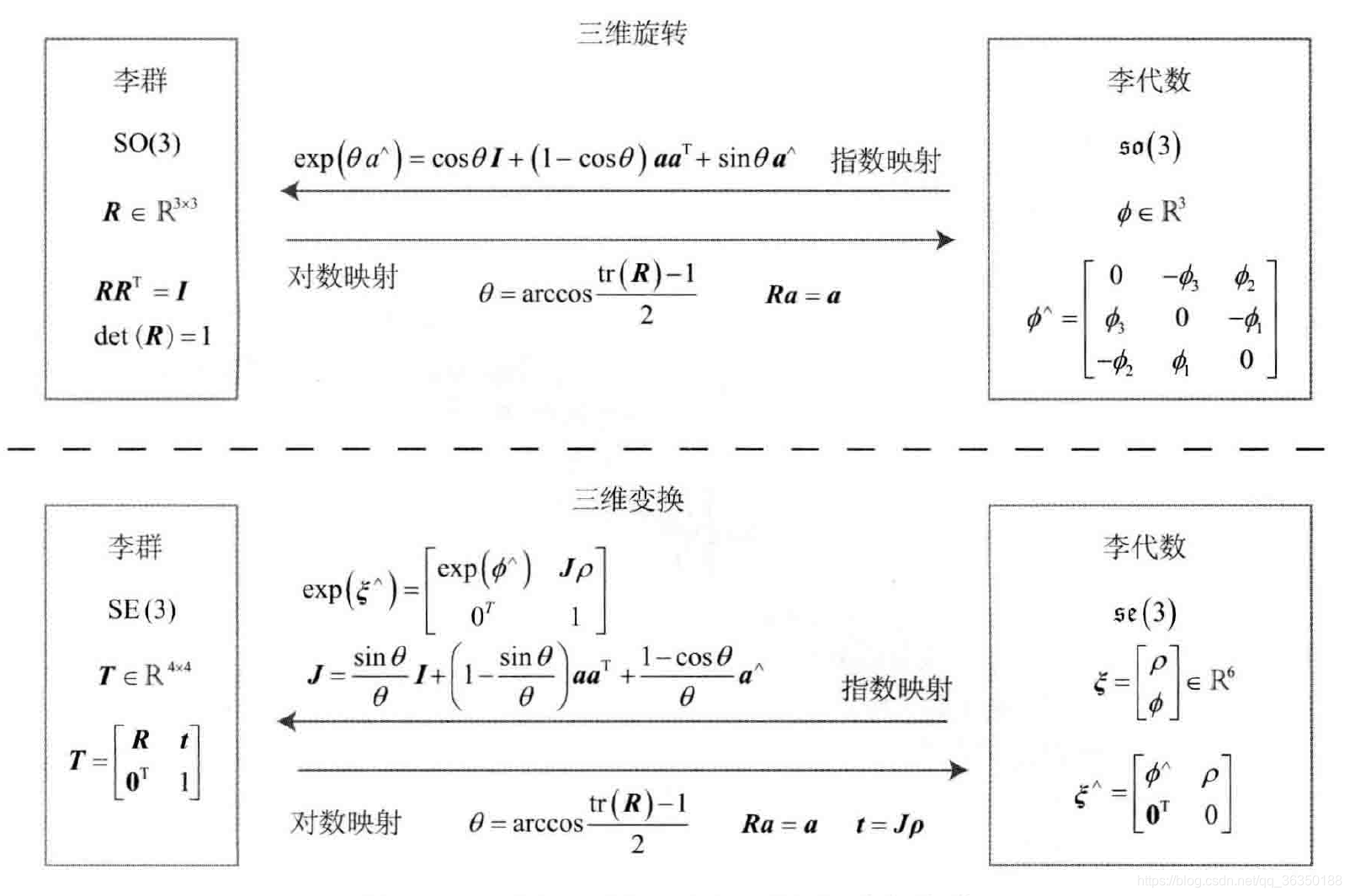

本文主要参考《视觉SLAM十四讲》