线性降维与统计学习理论（Linear Dimensionality Reduction & Statistical Learning Theory）

线性降维（Linear Dimensionality Reduction）（以PCA为例）

引入

主成分分析（Principal Component Analysis，PCA）是最常见的线性降维方法。

拿之前的线性回归举例，对于最小二乘法的线性回归，其求解参数为：$\hat{w}=(\hat{X}\hat{X})^{-1}\hat{X}y$其中$\hat{X}\in \mathcal{R}^{d\times n}$，$y\in \mathcal{R}^{n\times 1}$。
若直接求解$d\times d$的逆矩阵，其复杂度为$O(d^3)$，所以我们就想找到一个新的维度$d^{new}$，使其远小于原维度，即$d^{new}<<d$，但又不能对结果造成很大的影响。
这就引出了PCA，我们要抓住数据的”本质“。

具体讲解

现假设我们的原始数据$X=\left\{x_1,…,x_n\right\}$，以第$i$个数据为例，其维度为：$x^i\in \mathcal{R}^M$
然后这第$i$个数据的低纬度表示法为：$a^i\in \mathcal{R}^D, \quad D<<M$现在要做的就是找到个映射满足：$x^i \rightarrow a^i$
现在我们限制这样的映射为线性方程，即：$a^i=Bx^i, \quad B\in \mathcal{R}^{D\times M}$
———————————————————————————————————————

在继续之前先补充一个知识点，即是说，任何向量我们都可以改写成下面这样：$\pmb{x}=\sum_{i=1}^{M}a_i\pmb{u}_i, \quad其中 \pmb{u}_i^T\pmb{u}_j=\delta_{ij}$
当$i=j$时，$\delta_{ij}=1$，否则等于0，$u_i$与$u_j$正交。举个例子如下：

其中标量参数$a$可作如下表述：

也就是说，这个$a_i$是一个投影结果。

————————————————————————————————————————

所以原始向量我们可以写成如下两部分相加的形式：$x^n=\sum_{i=1}^{D}a_i\pmb{u}_i+\sum_{j=D+1}^{M}b_j\pmb{u}_j\approx\tilde{x}^n$其中第一部分就是我们想要的降维后的数据，第二部分是一些$error$组成的数据。这里的$\tilde{x}^n$是我们降维之后的数据，也就是第一部分。
我们选择$D$的标准是最小化数据的均方差，即是：

我们现在要最小化这个$error$，首先对$error$进行改写：

把上图的结论写下来：$E(u)=\sum_{n=1}^N||x^n||^2-(u^Tx^n)^2=\sum^N_{n=1}||x^n||^2-(a^n)^2$
最小化这个函数就等同于最大化后面的那个部分，也可以称为最大化投影的方差，这也就是PCA的基本思想，可以想象成把数据投影到直线上（跟另一篇分类问题里提到的有些类似），然后让数据尽可能分开，也就是让方差尽量大。
所以现在我们有：$\max \frac{1}{N}\sum_{n=1}^{N}a_n^2$注意，此处我们是假设均值为0的情况，否则则用下面的式子：$\max \frac{1}{N}\sum_{n=1}^{N}(a_n-\mu)^2$
但一般我们不会用上面这个，因为计算太麻烦，所以会事先让每个数据都减去均值，以保证零均值的情况，即是：$x^n-\overline{x}$
现在就可以写出如下形式的方程了：

根据这个图就能发现，把数据投影到$u_1$上能保留数据更多的信息。现在的问题就是如何找到这条轴，以及沿这条轴的数据的方差。
以下图为例：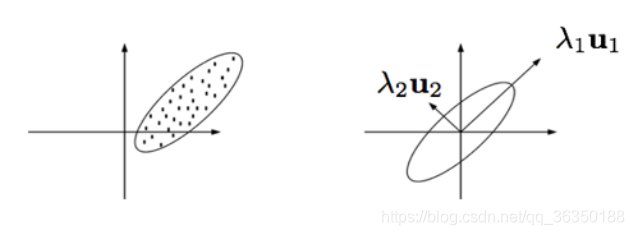

这里$\lambda_i$是沿方向$u_i$的边际方差（marginal variance）。

现假设如下数据，$X=[x^1,...,x^n]\in \mathcal{R}^{M\times N}$是一个有$N$个$M$维向量的矩阵，即$x^i\in\mathcal{R}^M$。另$u\in\mathcal{R}^M$为一个输入空间的方向，则第$j$个向量$x^j$在这个向量$u$上的投影为：$a_j=u^Tx^j=\sum_{i=1}{M}X_{ij}u_i$目标是找到一个方向$u$，使所有输入向量的投影的方差达到最大。\
首先计算所有投影的均值：$\overline{a}=\frac{1}{N}\sum^N_{j=1}a_j=\frac{1}{N}\sum_{j=1}^{N}\sum_{i=1}^{M}X_{ij}u_i=\sum^M_{i=1}u_i\mu_i$其中$\mu_i=\frac{1}{N}\sum^{N}_{j=1}X_{ij}$
计算方差为：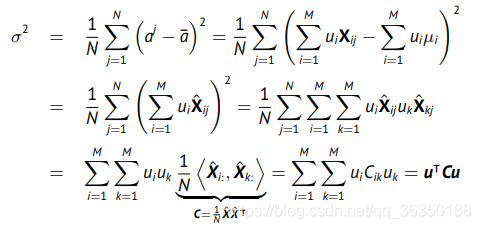

上面的方差也可以用另一个推导，意思一样但比较简洁：

其中$\pmb{C}$为协方差矩阵。在约束$||u||^2=1$下最大化这个方差，带约束的优化问题就得看拉格朗日了。如下：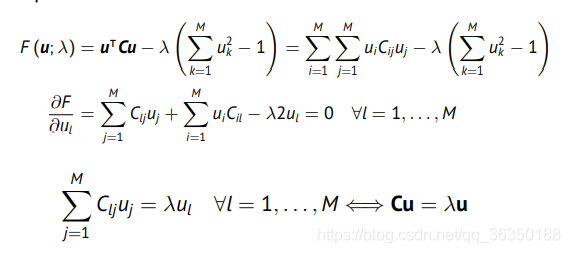

然后就很神奇地出现了特征值-特征向量的等式，其中最大的特征值就是最大方差，其对应的特征向量就是最大方差的方向。\
根据上面的结论可得：$\pmb{CU}=\pmb{U}\Lambda$，其中$\Lambda=diag(\lambda_1,…,\lambda_m)$，$\pmb{U}=[\pmb{u_1,…,u_M}]$，分别为特征值构成的对角矩阵以及特征向量构成的矩阵

注意，这里我们假设矩阵$\pmb{U}$是正交的，也就是范数为1，且这个对角矩阵的特征值已经按照从大到小排列了

然后我们就能把协方差矩阵$\pmb{C}$进行分解：$\pmb{C}=\pmb{U}\Lambda\pmb{U}^{-1}$$$$\pmb{C}=\pmb{U}\Lambda\pmb{U}^{T}$
如下图：

根据协方差矩阵的定义我们还知道，矩阵$\pmb{C}$是一个正的实对称矩阵。\
对于极小（约等于0）的特征值以及其对应的特征向量，我们就直接舍去，因为他们对于矩阵的信息作用不大。借助提取的特征值我们就能重新构造新的数据集，如下：
这种方法计算出来的满足 最小均方误差，即：$\min E(\pmb{u_1,...,u_D})=\sum_{n=1}^{N}||\pmb{x}^n-\tilde{\pmb{x}}^n||^2$
现在这个降维过程就以及大致结束了，做个总结，其步骤大致是：

1. 数据标准化（求解并减去均值）\
2. 求解协方差矩阵并进行分解，提取前$D$个特征值对应的特征向量（特征值已从大到小排列）\
3. 用如下方法重构数据：\
   
4. 有时也会将每个维度的方差归一.

现在还剩最后一个问题：怎么选择维度$D$？\
$D$越大的话近似效果越好，极端情况就是$D=M$，但这就没意义了。\
选择维度$D$一般有以下两种考量：

1. 看表现效果，当选取某维度达到我们需要的效果时，就选这个维度$D$；\
2. 事先定一个值，比如0.9，然后按照下面公式选取所需维度：
   

PCA的总结与应用

总结：

PCA将数据映射到线性子空间内\
PCA最大化映射的方差\
PCA最小化重构误差

应用：

PCA允许我们将高维的输入空间转化为低维的特征空间，同时捕捉到数据的本质\
PCA为数据找到一个更自然的坐标系(more natural coordinate)\
PCA 常用于高维输入数据的预处理

统计学习理论（Statistical Learning Theory）

统计学习理论的目的是：我们一开始并不知道正确的模型，而是需要从一组模型中选一个最优的。\
这里的最优指的是模型的泛化能力，即不能只在训练数据上误差最小。\
既然提到了这类优化，就得引入一个概念——风险（Risk）。
现在我们有一个损失函数：$L(y,f(x,w))$则其经验风险（Empirical risk）为：$R_{emp}(w)=\frac{1}{N}\sum_{i=1}^{N}L(y_i,f(x_i,w))$这里的$N$是数据点的数量。\
举个例子，对于二次方的损失函数，可表示为：$R_{emp}(w)=\frac{1}{N}\sum_{i=1}^{N}(y_i-f(x_i,w))^2$

但在现实中，我们更关注真实风险（True Risk）：$R(w)=\int L(y,f(x,w))p(x,y)dxdy=E_{x,y\sim p(x,y)}[L(y,f(x,w))]$这里的$p(\pmb{x},y)$是$\pmb{x}$和$y$的联合概率密度。\
由这个式子可以看出，这个风险是所有数据集的预期误差，是泛化误差的均值。\
但这里有一个问题，虽然$p(x,y)$是确定的，但我们通常无法知道，也就是说我们不能直接计算这个真实风险。

关于经验误差和真实误差，下面这个图就能很好说明了：

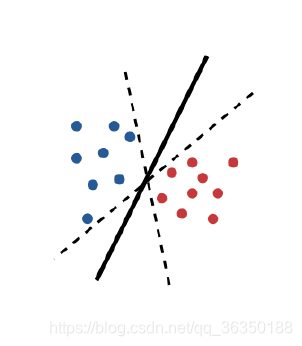
这三条边界都很好地把数据分开了，也就是说经验误差都是0，但用于测试时效果很可能会有很大差别。

经验风险与真实风险的对比

真实风险：\
优点：具有衡量泛化的能力\
缺点：通常我们不知道$p(\pmb{x},y)$

经验风险：\
优点：不需要知道$p(\pmb{x},y)$\
缺点：无法直接衡量泛化能力\
（学习算法通常时最小化经验误差）

当数据的分布非常集中，经验风险可以通过蒙特卡洛采样和求平均近似表示真实风险，当数据集无限大时，这种近似效果会很好。
现给出如下这个图：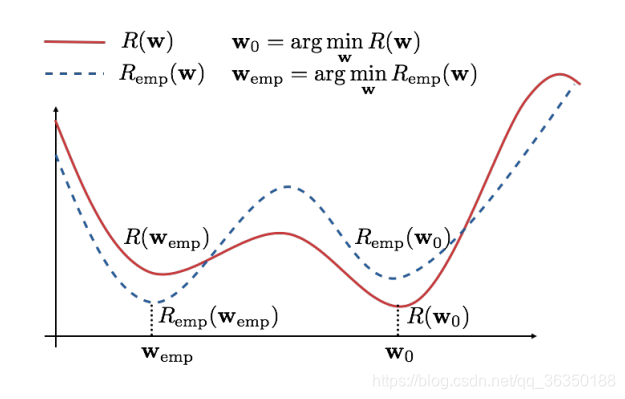

有如下两个假设：

1. 当训练数据越来越多时，经验风险会收敛于真实风险；\
2. 收敛是均匀的。

也就是说有如下两个式子：


其中的inf, sup分别表示下限和上限。
如果收敛是均匀的，则：

（这里多说一句，如果训练数据很多的话，这个$p^$是趋近于0的）
对于$(1-p^)$的情况，则有：

根据上面式子以及那副曲线图，可得：

以上就是收敛特性的推导过程。这里有个重要的充要条件：均匀收敛。\
经验风险最小化保证了当$N\rightarrow \infty$时真实风险也最小。

风险边界（Risk Bound）

思想就是：根据经验风险确定真实风险的上限，也就是说：$R(w)\leq R_{emp}(w)+\epsilon(N,p^*,h)$其中：$N$是训练数据总数；$p^*$是遇到边界的概率；$h$是学习机的学习能力，称为VC维度（VC-dimension）。
学习能力（Learning Power）可用下面这幅图解释：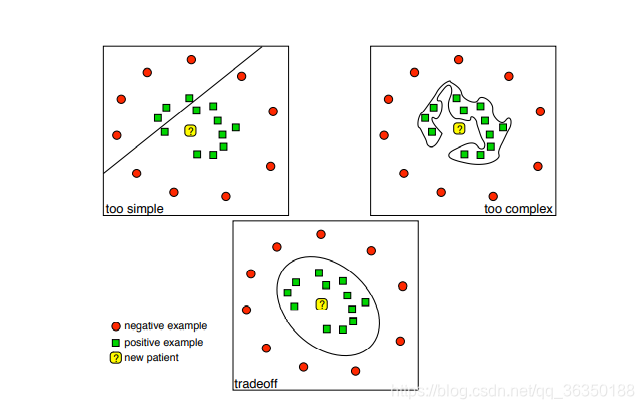

就是模型的复杂程度

VC-dimension

VC全程是Vapnik-Chervonenkis，大概定义就是：

一个函数族的VC维度是指能够被该函数族正确分类的数据点的最大数量（无论数据点的标签配置如何）。
VC维度是对一个分类器的分类能力或者说 “学习能力 “的衡量。

VC维度的确定：对于$\mathcal{R}^n$的线性分类器（超平面），VC维度为$n+1$。比如说，对于下图所示的线性分类器($\mathcal{R}^2$)，维度为3.

（注：上面这种确定方法只能说是对大多数情况都有效的，但不是全部。）

(这篇还未写完，后面关于VC维度的其余概念，不太明白在干嘛，先放着，以后有想法了再补充 )